题目内容
某商店经营甲、乙两种商品,其进价和售价如下表:
已知该商店购进了甲、乙两种商品共160件.
(1)若商店在销售完这批商品后要获利1000元,则应分别购进甲、乙两种商品各多少件?
(2)若商店的投入资金少于4300元,且要在售完这批商品后获利不少于1250元,则共有几种购货的方案?其中,哪种购货方案获得的利润最大?
| 甲 | 乙 | |
| 进价(元/件) | 15 | 35 |
| 售价(元/件) | 20 | 45 |
(1)若商店在销售完这批商品后要获利1000元,则应分别购进甲、乙两种商品各多少件?
(2)若商店的投入资金少于4300元,且要在售完这批商品后获利不少于1250元,则共有几种购货的方案?其中,哪种购货方案获得的利润最大?
考点:一元一次不等式组的应用,二元一次方程组的应用
专题:
分析:(1)等量关系为:甲件数+乙件数=160;甲总利润+乙总利润=1100.
(2)设出所需未知数,甲进价×甲数量+乙进价×乙数量≤4300.
(2)设出所需未知数,甲进价×甲数量+乙进价×乙数量≤4300.
解答:(1)设商店甲、乙两种商品分别购进了x件、y件,
由题意得
解得
答:商店甲、乙两种商品分别购进了120件、40件;
(2)设商店甲商品购进了z件,则乙商品购进了(160-z)件,
由题意得:
解得 65<z≤70
∴z的整数值为66,67,68,69,70.
即共有5种购货的方案:
①甲购进66件、乙购进94件,
②甲购进67件、乙购进93件,
③甲购进68件、乙购进92件,
④甲购进69件、乙购进91件,
⑤甲购进70件、乙购进90件.
其中,购货方案①获得的利润最大.
由题意得
|
解得
|
答:商店甲、乙两种商品分别购进了120件、40件;
(2)设商店甲商品购进了z件,则乙商品购进了(160-z)件,
由题意得:
|
解得 65<z≤70
∴z的整数值为66,67,68,69,70.
即共有5种购货的方案:
①甲购进66件、乙购进94件,
②甲购进67件、乙购进93件,
③甲购进68件、乙购进92件,
④甲购进69件、乙购进91件,
⑤甲购进70件、乙购进90件.
其中,购货方案①获得的利润最大.
点评:此题主要考查了二元一次方程组的应用以及一元一次不等式的应用,解决本题的关键是读懂题意,找到所求量的等量关系及符合题意的不等关系式组:甲件数+乙件数=160;甲总利润+乙总利润=1000.1250≤甲进价×甲数量+乙进价×乙数量<4300.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
 如图,四边形ABCD是平行四边形,E,F为对角线AC上两点,连接ED,EB,FD,FB.给出以下结论:①BE∥DF;②BE=DF;③AE=CF.请你从中选取一个条件,使∠1=∠2成立,并给出证明.
如图,四边形ABCD是平行四边形,E,F为对角线AC上两点,连接ED,EB,FD,FB.给出以下结论:①BE∥DF;②BE=DF;③AE=CF.请你从中选取一个条件,使∠1=∠2成立,并给出证明. 如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,点G为对角线交点,顶点A在x轴上,顶点C的坐标为(0,6),∠COB=30°,以OC上一点P为圆心,以
如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,点G为对角线交点,顶点A在x轴上,顶点C的坐标为(0,6),∠COB=30°,以OC上一点P为圆心,以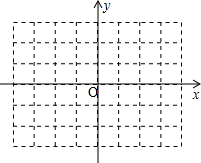 (1)在给出的直角坐标系中,画出两条一次函数图象,使得它们都满足;当自变量-1≤x≤1时,其函数值的取值范围为-2≤y≤3;
(1)在给出的直角坐标系中,画出两条一次函数图象,使得它们都满足;当自变量-1≤x≤1时,其函数值的取值范围为-2≤y≤3; 如图,Rt△ABC中,斜边上的中线CF=8cm,则中位线DE=
如图,Rt△ABC中,斜边上的中线CF=8cm,则中位线DE=