题目内容
18．先化简，再求值：（1-$\frac{1}{a+1}$）+$\frac{a}{{a}^{2}+2a+1}$，其中a=$\sqrt{3}-1$．分析 首先根据分式的混合运算法则化简此分式，然后将a=$\sqrt{3}-1$代入求值即可求得答案．
解答 解：（1-$\frac{1}{a+1}$）+$\frac{a}{{a}^{2}+2a+1}$，
=$\frac{a}{a+1}$+$\frac{a}{（a+1）^{2}}$，
=$\frac{a（a+2）}{（a+1）^{2}}$，
把a=$\sqrt{3}-1$代入，得
原式=$\frac{（\sqrt{3}-1）（\sqrt{3}-1+2）}{（\sqrt{3}-1+1）^{2}}$=$\frac{（\sqrt{3}）^{2}-1}{（\sqrt{3}）^{2}}$=$\frac{2}{3}$．
点评 本题考查了分式的化简求值．代入求值时，需要熟悉平方差公式．
练习册系列答案
相关题目
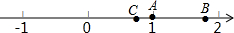如图所示，数轴上表示1和$\sqrt{3}$对应点分别为A、B，点B到点A的距离等于点C到点O的距离相等，设点C表示的数为x．
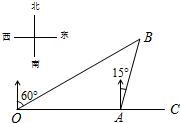如图，港口A在观测站O的正东方向，OA=40海里，某船从港口A出发，沿北偏东15°方向航行半小时后到达B处，此时从观测站O处测得该船位于北偏东60°的方向．求该船航行的速度．
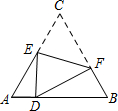如图，D是等边△ABC边AB上的一点，且AD：DB=1：3，现将△ABC折叠，使点C与D重合，折痕为EF，点E，F分别在AC和BC上，则CE：CF=5：7．
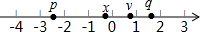x、y、p、q在数轴上的位置如图所示，则点（$\frac{x+1}{y}$，$\frac{p+2}{q}$）在平面直角坐标系xOy的第四象限．