Question

13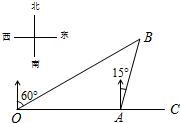．如图，港口A在观测站O的正东方向，OA=40海里，某船从港口A出发，沿北偏东15°方向航行半小时后到达B处，此时从观测站O处测得该船位于北偏东60°的方向．求该船航行的速度．

Answer 1

分析 过点A作AD⊥OB于D．先解Rt△AOD，得出AD=$\frac{1}{2}$OA=2海里，再由△ABD是等腰直角三角形，得出BD=AD=2海里，则AB=$\sqrt{2}$AD=2$\sqrt{2}$海里．结合航行时间来求航行速度．

解答 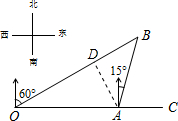解：过点A作AD⊥OB于点D．
在Rt△AOD中，∵∠ADO=90°，∠AOD=30°，OA=40海里，
∴AD=$\frac{1}{2}$OA=20海里．
在Rt△ABD中，∵∠ADB=90°，∠B=∠CAB-∠AOB=75°-30°=45°，
∴∠BAD=180°-∠ADB-∠B=45°=∠B，
∴BD=AD=20（海里），
∴AB=$\sqrt{A{D}^{2}+B{D}^{2}}$=$\sqrt{2}$AD=20$\sqrt{2}$（海里）．
∴该船航行的速度为20$\sqrt{2}$÷0.5=40$\sqrt{2}$（海里/小时），
答：该船航行的速度为40$\sqrt{2}$海里/小时．

点评 本题考查了解直角三角形的应用-方向角问题，难度适中，作出辅助线构造直角三角形是解题的关键．