Question

9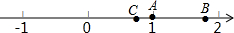．如图所示，数轴上表示1和$\sqrt{3}$对应点分别为A、B，点B到点A的距离等于点C到点O的距离相等，设点C表示的数为x．
（1）请你写出数x的值；
（2）求（x-$\sqrt{3}$）²的立方根．

Answer 1

分析 （1）根据数轴上两点间的距离求出AB之间的距离即为x的值；
（2）把x的值代入所求代数式进行计算即可．

解答 解：（1）∵点A、B分别表示1，$\sqrt{3}$，
∴AB=$\sqrt{3}$-1，即x=$\sqrt{3}$-1；
（2）∵x=$\sqrt{3}$-1，
∴（x-$\sqrt{3}$）²=（$\sqrt{3}$-1-$\sqrt{3}$）²=（-1）²=1，
故（x-$\sqrt{3}$）²的立方根为1．

点评 本题考查的是实数与数轴及两点间的距离，熟知实数与数轴上的点是一、一对应关系是解答此题的关键．