题目内容
11.如果三角形有一边上的中线恰好等于这边的长,那么称这个三角形为“匀称三角形”.(1)已知:如图1,在△ABC中,∠C=90°,BC=2$\sqrt{3}$,AB=2$\sqrt{7}$,求证:△ABC是“匀称三角形”;
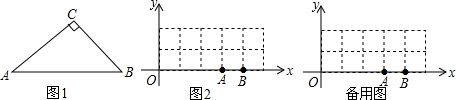
(2)在平面直角坐标系xOy中,如果三角形的一边在x轴上,且这边的中线恰好等于这边的长,我们又称这个三角形为“水平匀称三角形”.如图2,现有10个边长是1的小正方形组成的长方形区域记为G,每个小正方形的顶点称为格点,A(3,0),B(4,0),若C、D(C、D两点与O不重合)是x轴上的格点,且点C在点A的左侧.在G内使△PAC与△PBD都是“水平匀称三角形”的点P共有几个?其中是否存在横坐标为整数的点P,如果存在请求出这个点P的坐标,如果不存在请说明理由.
分析 (1)作AC边的中线BD交AC于点D,运用勾股定理求出BD,AC=BD得出△ABC是“匀称三角形”.
(2)①在G内使△PAC与△PBD都是“水平匀称三角形”的点P共有4个.利用图形表示出各点.
②在G内使△PAC与△PBD都是“水平匀称三角形”的点P中,存在横坐标为整数的点P.第四种情况,运用△PAC与△PBD都是“水平匀称三角形”得出P点横坐标为整数3.
解答 解:(1)如图1,作AC边的中线BD交AC于点D,
∵∠C=90°,BC=2$\sqrt{3}$,AB=2$\sqrt{7}$,
∴AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=4.
∴AD=CD=2.
BD=$\sqrt{C{D}^{2}+B{C}^{2}}$=4,
∴AC=BD,
∴△ABC是“匀称三角形”;
(2)①在G内使△PAC与△PBD都是“水平匀称三角形”的点P共有4个.
如图:
第一种如图2,点C(1,0),点D(3,0)与A重合,用圆的交点找点P,
第二种如图3,点C(1,0),点D(2,0)
第三种如图4,点C(1,0),点D(5,0)
第四种如图5,当C点坐标为(2,0),D点坐标为(3,0)与A重合时,
②在G内使△PAC与△PBD都是“水平匀称三角形”的点P中,存在横坐标为整数的点P.
第四种情况,如图5,当C点坐标为(2,0),D点坐标为(3,0)与A重合时,△PAC与△PBD是水平匀称三角形.
∵A(3,0),C(2,0),
B(4,0),D(3,0)
∴AC=1,BD=1
设PM、PN分别为CA、DB上的中线,
∴AM=$\frac{1}{2}$AC=$\frac{1}{2}$,
AN=$\frac{1}{2}$BD=$\frac{1}{2}$,
∴AM=AN=$\frac{1}{2}$,
∴点A为MN的中点.
∵△PAC与△PBD是“水平匀称三角形”,
∴PM=AC=1,PN=BD=1,
∴PM=PN=1,
∴PA⊥MN,即PA与x轴垂直,
∵A(3,0)
∴P点横坐标为整数3.
在Rt△PMA中,PM=1,AM=$\frac{1}{2}$,
∴PA=$\frac{\sqrt{3}}{2}$,
∴P(3,$\frac{\sqrt{3}}{2}$)
所以,当C点坐标为(2,0),D点坐标为(3,0)与A重合时,△PAC与△PBD是水平匀称三角形且P点横坐标为整数.
点评 本题主要考查了几何变换综合题,题目给出了新的定义即“匀称三角形”和“水平匀称三角形”,解题的关键是理解定义并能正确运用定义解题.

 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案| A. | 5,12,13 | B. | 4,5,9 | C. | 2,3,$\sqrt{5}$ | D. | 1,$\sqrt{2}$,$\sqrt{3}$ |
| A. | 同旁内角互补,两直线平行 | |
| B. | 直线a⊥b,则a 与b的夹角为直角 | |
| C. | 如果两个角互补,那么这两个角一个是锐角,一个是钝角 | |
| D. | 若a∥b,a⊥c,那么b⊥c |
| A. | $\frac{5}{4}$ | B. | $\frac{5}{3}$ | C. | $\frac{20}{9}$ | D. | $\frac{12}{5}$ |
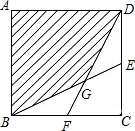 已知四边形ABCD为正方形,E、F分别为边BC、CD的中点,AD=1,求阴影部分的面积.
已知四边形ABCD为正方形,E、F分别为边BC、CD的中点,AD=1,求阴影部分的面积.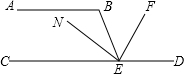 如图,AB∥CD,点E在CD上,EN平分∠BEC,EF⊥EN.若∠B=110°,则∠DEF=55°.
如图,AB∥CD,点E在CD上,EN平分∠BEC,EF⊥EN.若∠B=110°,则∠DEF=55°.