题目内容
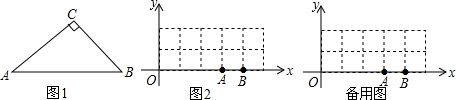
2．在三边分别为下列长度的三角形中，不是直角三角形的是（ ）| A． | 5，12，13 | B． | 4，5，9 | C． | 2，3，$\sqrt{5}$ | D． | 1，$\sqrt{2}$，$\sqrt{3}$ |
分析 由勾股定理的逆定理，只要验证两小边的平方和等于最长边的平方即可．
解答 解：A、52+122=132，故能构成三角形，故此选项错误；
B、42+52≠92，故不能构成三角形，故此选项正确；
C、22+（$\sqrt{5}$）2=32，故能构成三角形，故此选项错误；
D、12+（$\sqrt{2}$）2=（$\sqrt{3}$）2，故能构成三角形，故此选项错误；
故选：B．
点评 本题考查勾股定理的逆定理的应用．判断三角形是否为直角三角形，已知三角形三边的长，只要利用勾股定理的逆定理加以判断即可
练习册系列答案
相关题目
5．把一条弯曲的公路改成直道，可以缩短路程，用数学知识解释其道理，正确的是（ ）
| A． | 两点确定一条直线 | B． | 两点之间，线段最短 | ||
| C． | 两点确定一条线段 | D． | 两点之间，直线最短 |
13．如图所示，将8个一样大的矩形（长为a cm，宽b cm）拼图，拼出了如图甲、乙的两种图案．图案甲是一个正方形，图乙是一个长方形，则图甲的中间阴影部分面积为（ ）
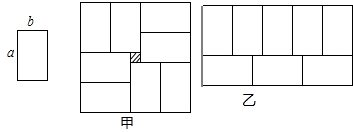
| A． | （a+2b）2 | B． | $\frac{{b}^{2}}{9}$ | C． | （a-b）2 | D． | a2-b2 |
17．
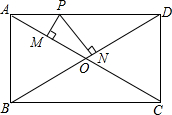如图，矩形ABCD中，对角线AC与BD相交于点O，P为AD上的动点，过点P作PM⊥AC，PN⊥BD，垂足分别为M、N，若AB=m，BC=n，则PM+PN=（ ）
如图，矩形ABCD中，对角线AC与BD相交于点O，P为AD上的动点，过点P作PM⊥AC，PN⊥BD，垂足分别为M、N，若AB=m，BC=n，则PM+PN=（ ）| A． | $\frac{m+n}{2}$ | B． | $\frac{mn}{m+n}$ | C． | $\frac{mn}{{\sqrt{m_{\;}^2+{n^2}}}}$ | D． | $\frac{n}{m}$ |
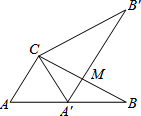如图，△ABC中，∠ACB=90°，∠B=30°，BC=6，三角板绕C逆时针旋转，当点A的对应点A′落在AB边上时即停止转动，则BM的长为3．
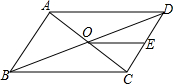如图?ABCD中，AC、BD交于点O，E是CD边的中点，连接OE，若?ABCD周长为20，BD=8，则△ODE的周长为9．