题目内容
1. 已知四边形ABCD为正方形,E、F分别为边BC、CD的中点,AD=1,求阴影部分的面积.
已知四边形ABCD为正方形,E、F分别为边BC、CD的中点,AD=1,求阴影部分的面积.
分析 连接BD,可看出阴影部分的面积等于$\frac{1}{2}$正方形的面积+一个三角形的面积,用相似求出三角形的面积,阴影部分的面积可证.
解答 解:连接BD,EF.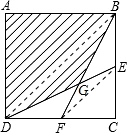
∵阴影部分的面积=△ABD的面积+△BDG的面积,
∴△ABD的面积=$\frac{1}{2}$正方形ABCD的面积=$\frac{1}{2}$×12=$\frac{1}{2}$,
∵△BCD中EF为中位线,
∴EF∥BD,EF=$\frac{1}{2}$BD,
∴△GEF∽△GBD,
∴DG=2GE,
∴△BDE的面积=$\frac{1}{2}$△BCD的面积.
∴△BDG的面积=$\frac{2}{3}$△BDE的面积=$\frac{1}{3}$△BCD的面积=$\frac{1}{3}$×$\frac{1}{2}$×12=$\frac{1}{6}$.
∴阴影部分的面积=$\frac{1}{2}$+$\frac{1}{6}$=$\frac{2}{3}$.
点评 本题考查正方形的性质,正方形的四个边长相等,关键是连接BD,把阴影部分分成两部分计算.

练习册系列答案
相关题目
5.把一条弯曲的公路改成直道,可以缩短路程,用数学知识解释其道理,正确的是( )
| A. | 两点确定一条直线 | B. | 两点之间,线段最短 | ||
| C. | 两点确定一条线段 | D. | 两点之间,直线最短 |
13.如图所示,将8个一样大的矩形(长为a cm,宽b cm)拼图,拼出了如图甲、乙的两种图案.图案甲是一个正方形,图乙是一个长方形,则图甲的中间阴影部分面积为( )
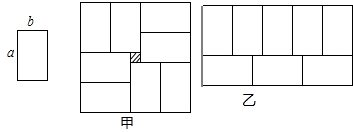

| A. | (a+2b)2 | B. | $\frac{{b}^{2}}{9}$ | C. | (a-b)2 | D. | a2-b2 |
 如图,正方形ABCD的边长为3,以直线AB为轴,将正方形旋转一周,从正面看所得图形的周长是18.
如图,正方形ABCD的边长为3,以直线AB为轴,将正方形旋转一周,从正面看所得图形的周长是18.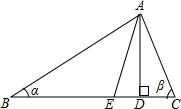 如图在△ABC中,AD是BC边上的高线,AE是△ABC的角平分线,若∠B=α,∠C=β(α<β),用含α,β的代数式表示∠EAD.
如图在△ABC中,AD是BC边上的高线,AE是△ABC的角平分线,若∠B=α,∠C=β(α<β),用含α,β的代数式表示∠EAD.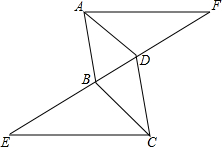 如图所示,△ADF≌△CBE,且点E,B,D,F在一条直线上,判断AD与BC的位置关系,并说明理由.
如图所示,△ADF≌△CBE,且点E,B,D,F在一条直线上,判断AD与BC的位置关系,并说明理由.