题目内容
6.已知:关于x的方程mx2+(3m+1)x+3=0.(1)求证:不论m为任何实数,此方程总有实数根;
(2)如果该方程有两个不同的整数根,且m为正整数,求m的值.
分析 (1)分类讨论m=0和m≠0两种情况下方程根的个数;
(2)把mx2+(3m+1)x+3=0因式分解得到x1=-$\frac{1}{m}$,x2=-3,根据题意可知-$\frac{1}{m}$是整数,据此求出正整数m的值.
解答 (1)证明:当m=0时,x=-3,
当m≠0时,b2-4ac=(3m-1)2≥0,
所以 该一元二次方程有两个实根,
综上不论m为何实数,此方程总有实数根;
(2)解:∵mx2+(3m+1)x+3=0,
∴(mx+1)(x+3)=0,
∴x1=-$\frac{1}{m}$,x2=-3,
∵方程有两个不同的整数根,且m为正整数,
∴m=1.
点评 本题主要考查了根的判别式的知识,解答本题要掌握一元二次方程根的情况与判别式△的关系:(1)△>0?方程有两个不相等的实数根;(2)△=0?方程有两个相等的实数根;(3)△<0?方程没有实数根.

练习册系列答案
相关题目
17.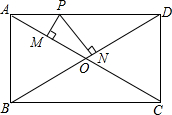 如图,矩形ABCD中,对角线AC与BD相交于点O,P为AD上的动点,过点P作PM⊥AC,PN⊥BD,垂足分别为M、N,若AB=m,BC=n,则PM+PN=( )
如图,矩形ABCD中,对角线AC与BD相交于点O,P为AD上的动点,过点P作PM⊥AC,PN⊥BD,垂足分别为M、N,若AB=m,BC=n,则PM+PN=( )
 如图,矩形ABCD中,对角线AC与BD相交于点O,P为AD上的动点,过点P作PM⊥AC,PN⊥BD,垂足分别为M、N,若AB=m,BC=n,则PM+PN=( )
如图,矩形ABCD中,对角线AC与BD相交于点O,P为AD上的动点,过点P作PM⊥AC,PN⊥BD,垂足分别为M、N,若AB=m,BC=n,则PM+PN=( )| A. | $\frac{m+n}{2}$ | B. | $\frac{mn}{m+n}$ | C. | $\frac{mn}{{\sqrt{m_{\;}^2+{n^2}}}}$ | D. | $\frac{n}{m}$ |
18.在平面直角坐标系中,点M(-5,-3m+4)在第三象限,则m的取值范围是( )
| A. | m<$\frac{4}{3}$ | B. | m>-$\frac{4}{3}$ | C. | m>$\frac{4}{3}$ | D. | m<-$\frac{4}{3}$ |
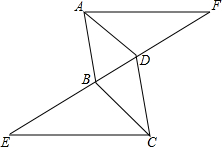 如图所示,△ADF≌△CBE,且点E,B,D,F在一条直线上,判断AD与BC的位置关系,并说明理由.
如图所示,△ADF≌△CBE,且点E,B,D,F在一条直线上,判断AD与BC的位置关系,并说明理由.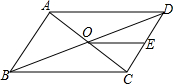 如图?ABCD中,AC、BD交于点O,E是CD边的中点,连接OE,若?ABCD周长为20,BD=8,则△ODE的周长为9.
如图?ABCD中,AC、BD交于点O,E是CD边的中点,连接OE,若?ABCD周长为20,BD=8,则△ODE的周长为9.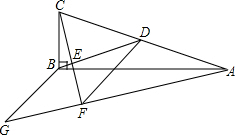 如图,在△ABC中,∠ABC=90°,点D为AC的中点,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接BG、DF.
如图,在△ABC中,∠ABC=90°,点D为AC的中点,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接BG、DF.
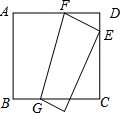 如图,将边长为12厘米的正方形ABCD折叠,使得A点落在CD上的E点,然后压平折痕FG,若FG的长为13厘米,则线段CE的长为( )
如图,将边长为12厘米的正方形ABCD折叠,使得A点落在CD上的E点,然后压平折痕FG,若FG的长为13厘米,则线段CE的长为( )