题目内容
13. 如图,已知DC=AB,AD=BC,点E、F在AC上,AE=CF.求证:DE∥BF.
如图,已知DC=AB,AD=BC,点E、F在AC上,AE=CF.求证:DE∥BF.
分析 由“SSS”证得△ABC≌△CDA,得出∠DAE=∠BCF,进一步求得△ADE≌△CBF,得出∠AED=∠CFB,即∠DEC=∠BFA,进而可求证DE与BF平行.
解答 解:∵在△ABC和△CDA中,
$\left\{\begin{array}{l}{AB=DC}\\{BC=AD}\\{BC=CB}\end{array}\right.$,
∴△ABC≌△CDA,
∴∠BCA=∠DAC,
在△ADE≌△CBF中,
$\left\{\begin{array}{l}{AD=BC}\\{∠DAE=∠BCF}\\{AE=CF}\end{array}\right.$,
∴△ADE≌△CBF,
∴∠AED=∠CFB,
∴∠DEC=∠BFA,
∴DE∥BF.
点评 此题考查三角形全等的判定与性质,平行线的判定,掌握三角形全等的判定方法是解决问题的关键.

练习册系列答案
相关题目
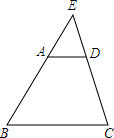 如图,在梯形ABCD中,AD∥BC,延长两腰交于点E,若AD=2,BC=6,AB=4,则$\frac{ED}{EC}$=$\frac{1}{3}$,$\frac{DE}{DC}$=$\frac{1}{2}$.
如图,在梯形ABCD中,AD∥BC,延长两腰交于点E,若AD=2,BC=6,AB=4,则$\frac{ED}{EC}$=$\frac{1}{3}$,$\frac{DE}{DC}$=$\frac{1}{2}$. 如图,在矩形ABCD中,AB=6米,BC=8米,动点P以2米/秒的速度从点A出发,沿AC向点C移动,同时动点Q以1米/秒的速度从点C出发,沿CB项点B移动,设P、Q两点移动t秒(0<t<5)后,三角形CPQ的面积为S米2.
如图,在矩形ABCD中,AB=6米,BC=8米,动点P以2米/秒的速度从点A出发,沿AC向点C移动,同时动点Q以1米/秒的速度从点C出发,沿CB项点B移动,设P、Q两点移动t秒(0<t<5)后,三角形CPQ的面积为S米2. 如图,向△ABC外作正方形ABEF和ACGH,点M是BC边的中点,求证:FH=2AM.
如图,向△ABC外作正方形ABEF和ACGH,点M是BC边的中点,求证:FH=2AM.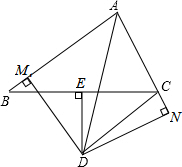 如图,在△ABC中,AD平分∠BAC,DE所在直线是BC的垂直平分线,E为垂足,过点D作DM⊥AB于点M,DN⊥AC交AC的延长线于点N.求证:
如图,在△ABC中,AD平分∠BAC,DE所在直线是BC的垂直平分线,E为垂足,过点D作DM⊥AB于点M,DN⊥AC交AC的延长线于点N.求证: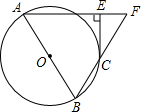 如图,AB为⊙O的直径,AE⊥CE于点E,BC的延长线与AE的延长线相交于点F.若CE为⊙O的切线,AF=BF,求∠A的度数.
如图,AB为⊙O的直径,AE⊥CE于点E,BC的延长线与AE的延长线相交于点F.若CE为⊙O的切线,AF=BF,求∠A的度数.