题目内容
5.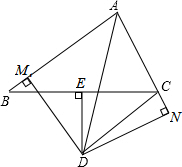 如图,在△ABC中,AD平分∠BAC,DE所在直线是BC的垂直平分线,E为垂足,过点D作DM⊥AB于点M,DN⊥AC交AC的延长线于点N.求证:
如图,在△ABC中,AD平分∠BAC,DE所在直线是BC的垂直平分线,E为垂足,过点D作DM⊥AB于点M,DN⊥AC交AC的延长线于点N.求证:(1)BM=CN;
(2)AM=$\frac{1}{2}$(AB+AC).
分析 (1)连接BD,利用线段垂直平分线的性质得出BD=CD,利用角平分线的性质得出DM=DN,进而证明△BMD与△CDN全等即可;
(2)利用△BMD与△CDN全等得出BM=CN,进而证明即可.
解答 证明:(1)连接BD,如图:
∵DE所在直线是BC的垂直平分线,
∴BD=CD,
∵AD平分∠BAC,过点D作DM⊥AB于点M,DN⊥AC交AC的延长线于点N,
∴DM=DN,
在Rt△BMD与Rt△CDN中,
$\left\{\begin{array}{l}{BD=DC}\\{DM=DN}\end{array}\right.$,
∴Rt△BMD≌Rt△CDN(HL),
∴BM=CN;
(2)∵Rt△BMD≌Rt△CDN,
∴BM=CN,AM=AN,
∴AB+AC=AM+BM+AN-CN=2AM,
∴AM=$\frac{1}{2}$(AB+AC).
点评 此题考查全等三角形的判定和性质,关键是证明△BMD与△CDN全等.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
16.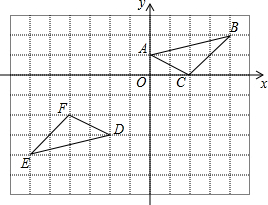 如图,在平面直角坐标系中,点A的坐标为(0,1),点B的坐标为(4,2),C的坐标为(2,0),将△ABC绕点P旋转180°得到△DEF,则旋转中心点P的坐标为( )
如图,在平面直角坐标系中,点A的坐标为(0,1),点B的坐标为(4,2),C的坐标为(2,0),将△ABC绕点P旋转180°得到△DEF,则旋转中心点P的坐标为( )
 如图,在平面直角坐标系中,点A的坐标为(0,1),点B的坐标为(4,2),C的坐标为(2,0),将△ABC绕点P旋转180°得到△DEF,则旋转中心点P的坐标为( )
如图,在平面直角坐标系中,点A的坐标为(0,1),点B的坐标为(4,2),C的坐标为(2,0),将△ABC绕点P旋转180°得到△DEF,则旋转中心点P的坐标为( )| A. | (-1,-1) | B. | (-1,-2) | C. | (-2,-1) | D. | (-2,-2) |
14.下面每组中的两个数互为相反数的是( )
| A. | -$\frac{1}{5}$和5 | B. | 8和-(-8) | C. | -2.5和2$\frac{1}{2}$ | D. | $\frac{1}{3}$和0.333 |
15.下列各点在抛物线y=-x2+1上的是( )
| A. | (1,2) | B. | (-1,0) | C. | (2,5) | D. | (3,-5) |
 如图,已知DC=AB,AD=BC,点E、F在AC上,AE=CF.求证:DE∥BF.
如图,已知DC=AB,AD=BC,点E、F在AC上,AE=CF.求证:DE∥BF. 四边形ABCD中,AD∥BC,AB⊥BC,E是AB上一点,且AD=BE,AE=BC,求证:△DEC是等腰直角三角形.
四边形ABCD中,AD∥BC,AB⊥BC,E是AB上一点,且AD=BE,AE=BC,求证:△DEC是等腰直角三角形.
 如图,是某校美术室的一个道具,它是由棱长均为10dm的小立方块搭成的,工人师傅要将其表面(底面除外)涂上油漆,请你计算一下,工人师傅至少需涂多少平方米的油漆?
如图,是某校美术室的一个道具,它是由棱长均为10dm的小立方块搭成的,工人师傅要将其表面(底面除外)涂上油漆,请你计算一下,工人师傅至少需涂多少平方米的油漆?