题目内容
1．
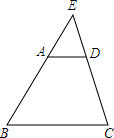如图，在梯形ABCD中，AD∥BC，延长两腰交于点E，若AD=2，BC=6，AB=4，则$\frac{ED}{EC}$=$\frac{1}{3}$，$\frac{DE}{DC}$=$\frac{1}{2}$．
分析 根据题意，直接写出比例式，即可解决问题．
解答 解：如图，∵AD∥BC，
∴$\frac{ED}{EC}$=$\frac{AD}{BC}=\frac{2}{6}=\frac{1}{3}$，
∴$\frac{DE}{DC}$=$\frac{1}{2}$．
故答案为：$\frac{1}{3}$，$\frac{1}{2}$．
点评 该题主要考查了平行线分线段成比例定理及其应用问题，准确找出图形中的对应线段是解题的关键．
练习册系列答案
名校课堂系列答案
相关题目
9．已知点A（0，-3）是抛物线y=-（n-1）x2+n的最低点，则抛物线与x轴两个交点之间的距离是（ ）
| A． | 1 | B． | $\sqrt{2}$ | C． | $\sqrt{3}$ | D． | 2$\sqrt{3}$ |
16．
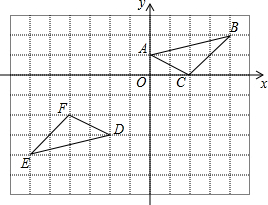如图，在平面直角坐标系中，点A的坐标为（0，1），点B的坐标为（4，2），C的坐标为（2，0），将△ABC绕点P旋转180°得到△DEF，则旋转中心点P的坐标为（ ）
如图，在平面直角坐标系中，点A的坐标为（0，1），点B的坐标为（4，2），C的坐标为（2，0），将△ABC绕点P旋转180°得到△DEF，则旋转中心点P的坐标为（ ）| A． | （-1，-1） | B． | （-1，-2） | C． | （-2，-1） | D． | （-2，-2） |
已知：如图，在△ABC中，DE∥BC，AD2=AE•AC，求证：
如图，已知DC=AB，AD=BC，点E、F在AC上，AE=CF．求证：DE∥BF．