Question

18．如图，向△ABC外作正方形ABEF和ACGH，点M是BC边的中点，求证：FH=2AM．

Answer 1

分析 在AM的延长线上取点N，使AM=MN，连接BN、CN，则四边形ABNC是平行四边形ABNC，得到CN=AB，∠BAC+∠ACN=180°，根据四边形ABEF、ACGH是正方形，易证AF=AB=CN，AH=AC，∠FAH=∠ACN，根据SAS证明△ACN≌△AHF即可证明FH=AN=2AM．

解答 证明：在AM的延长线上取点N，使AM=MN，连接BN、CN
∵M是BC的中点，AM=MN，
∴四边形ABNC是平行四边形ABNC，（对角线互相平分）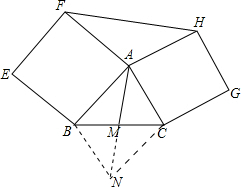
∴CN=AB，∠BAC+∠ACN=180°，
∵四边形ABEF、ACGH是正方形，
∴AF=AB，AH=AC，∠BAF=∠CAH=90°，
∴AF=CN，∠BAC+∠FAH=360°-∠BAF-∠CAH=180°，
∴∠FAH=∠ACN，
在△ACN和△AHF中，
 $\left\{\begin{array}{l}{AF=CN}\\{∠FAH=∠ACN}\\{AH=AC}\end{array}\right.$，
∴△ACN≌△AHF （SAS）
∴FH=AN，
∵AN=AM+MN=2AM，
∴FH=2AM．

点评 本题主要考查了全等三角形的判定与性质、正方形的性质以及平行四边形的判定与性质，作辅助线构造全等三角形和平行四边形是解决问题的关键．