题目内容
16.如图1,在Rt△ABC中,∠ACB=90°,O是AB上一点,以OA为半径的⊙O切BC于点D,交AC于点E,且AD=BD.(1)求证:DE∥AB;
(2)如图2,连接OC,求cos∠ACO的值.
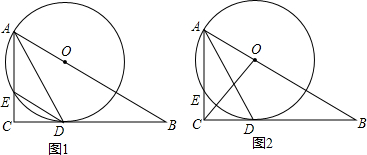
分析 (1)连结OD、OE,如图1,根据切线性质得OD⊥BC,则OD∥AC,所以∠2=∠3,加上∠1=∠3,则∠1=∠2,再利用AD=BD得到∠1=∠B,所以∠1=∠2=∠B,然后根据三角形内角和可计算出∠1=∠2=∠B=30°,于是可判断△OAE为等边三角形,得到AE=OE,再判断四边形AEDO为平行四边形,从而得到DE∥AB;
(2)作OH⊥AE于H,如图2,则AH=HE,设⊙O的半径为r,在Rt△AOH中利用含30度的直角三角形三边的关系得到OH=$\sqrt{3}$AH=$\frac{\sqrt{3}}{2}$r,易得四边形ODCH为矩形,则CH=OD=r,再利用勾股定理计算出OC=$\frac{\sqrt{7}}{2}$r,然后根据余弦的定义求解.
解答 (1)证明:连结OD、OE,如图1,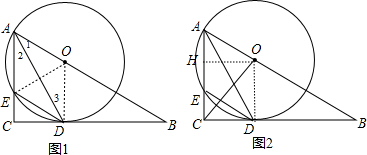 ∵BC为切线,
∵BC为切线,
∴OD⊥BC,
∵∠C=90°,
∴OD∥AC,
∴∠2=∠3,
∵OA=OD,
∴∠1=∠3,
∴∠1=∠2,
∵AD=BD,
∴∠1=∠B,
∴∠1=∠2=∠B,
∵∠1+∠2+∠B=90°,
∴∠1=∠2=∠B=30°,
∴△OAE为等边三角形,
∴AE=OE,
∴AE=OD,
∵AE∥OD,
∴四边形AEDO为平行四边形,
∴DE∥AB;
(2)解:作OH⊥AE于H,如图2,则AH=HE,
设⊙O的半径为r,
在Rt△AOH中,∵∠OAH=60°,
∴AH=$\frac{1}{2}$OA=$\frac{1}{2}$r,OH=$\sqrt{3}$AH=$\frac{\sqrt{3}}{2}$r,
易得四边形ODCH为矩形,
∴CH=OD=r,
在Rt△OCH中,OC=$\sqrt{O{H}^{2}+C{H}^{2}}$=$\sqrt{(\frac{\sqrt{3}}{2}r)^{2}+{r}^{2}}$=$\frac{\sqrt{7}}{2}$r,
∴cos∠HCO=$\frac{CH}{CO}$=$\frac{r}{\frac{\sqrt{7}r}{2}}$=$\frac{2\sqrt{7}}{7}$,
即cos∠ACO=$\frac{2\sqrt{7}}{7}$,
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.也考查了等腰三角形的性质和三角函数的定义.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案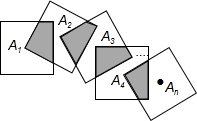 如图,将n个边长都为2的正方形按如图所示摆放,点A1,A2,…An分别是正方形的中心,则这n个正方形重叠部分的面积之和是( )
如图,将n个边长都为2的正方形按如图所示摆放,点A1,A2,…An分别是正方形的中心,则这n个正方形重叠部分的面积之和是( )| A. | n | B. | n-1 | C. | 4(n-1) | D. | 4n |
 如图,在△ABC中,AE是中线,AD是角平分线,AF是高,∠B=30°,∠C=80°,BE=3,AF=2,填空:
如图,在△ABC中,AE是中线,AD是角平分线,AF是高,∠B=30°,∠C=80°,BE=3,AF=2,填空: 如图,△ABC为等边三角形,D、E分别是AC、BC上的点,且AD=CE,AE与BD相交于点P,
如图,△ABC为等边三角形,D、E分别是AC、BC上的点,且AD=CE,AE与BD相交于点P, 某路基的横截面如图所示,路基高BC=1m,斜坡AB的坡度为1:2,则斜坡AB的长为$\sqrt{5}$m.
某路基的横截面如图所示,路基高BC=1m,斜坡AB的坡度为1:2,则斜坡AB的长为$\sqrt{5}$m. 如图,已知AB∥ED,∠B=120°,∠D=140°.求∠BCD的度数.
如图,已知AB∥ED,∠B=120°,∠D=140°.求∠BCD的度数. 如图,在△ABC中,AB=20,AC=30,∠BAC=120°,求S△ABC的值.
如图,在△ABC中,AB=20,AC=30,∠BAC=120°,求S△ABC的值. 如图,在平面直角坐标系中,抛物线y=ax2+bx-4a与直线y=-x+4交两坐标轴于点B,C,且与x轴交另一点A.
如图,在平面直角坐标系中,抛物线y=ax2+bx-4a与直线y=-x+4交两坐标轴于点B,C,且与x轴交另一点A.