题目内容
5. 如图,在△ABC中,AB=20,AC=30,∠BAC=120°,求S△ABC的值.
如图,在△ABC中,AB=20,AC=30,∠BAC=120°,求S△ABC的值.
分析 延长BA,过点C作CD⊥BA交于点D,首先根据邻补角互补计算出∠DAC=60°,再计算出∠ACD=30°,根据直角三角形的性质可得AD=$\frac{1}{2}$AC=2,然后利用勾股定理计算CD长,利用三角形的面积公式可得S△ABC.
解答 解:延长BA,过点C作CD⊥BA交于点D,
∵∠BAC=120°,
∴∠DAC=60°,
∴∠ACD=30°,
∵AC=30,
∴AD=15,
∴CD=$\sqrt{{AC}^{2}{-AD}^{2}}$=$\sqrt{{30}^{2}{-15}^{2}}$=15$\sqrt{3}$,
∴S△ABC=$\frac{1}{2}$•AB•CD=$\frac{1}{2}×20×15\sqrt{3}$=150$\sqrt{3}$.
点评 此题主要考查了勾股定理,关键是正确作出辅助线,掌握在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方.

练习册系列答案
相关题目
15.下列事件中必然发生的事件是( )
| A. | 一个图形平移后所得的图形与原来的图形不全等 | |
| B. | 100件产品中有4件次品,从中任意抽取5件,至少一件是正品 | |
| C. | 不等式的两边同时乘以一个数,结果仍是不等式 | |
| D. | 随意翻一本书的某页,这页的页码一定是偶数 |
10. 如图所示,河堤横断面堤高BC=$5\sqrt{3}$米,迎水坡面AB的坡度为$\frac{{\sqrt{3}}}{3}$(坡度是指坡面的铅直高度与水平宽度之比,又称坡比),则AC的长是( )
如图所示,河堤横断面堤高BC=$5\sqrt{3}$米,迎水坡面AB的坡度为$\frac{{\sqrt{3}}}{3}$(坡度是指坡面的铅直高度与水平宽度之比,又称坡比),则AC的长是( )
 如图所示,河堤横断面堤高BC=$5\sqrt{3}$米,迎水坡面AB的坡度为$\frac{{\sqrt{3}}}{3}$(坡度是指坡面的铅直高度与水平宽度之比,又称坡比),则AC的长是( )
如图所示,河堤横断面堤高BC=$5\sqrt{3}$米,迎水坡面AB的坡度为$\frac{{\sqrt{3}}}{3}$(坡度是指坡面的铅直高度与水平宽度之比,又称坡比),则AC的长是( )| A. | $5\sqrt{3}$米 | B. | 10米 | C. | 15米 | D. | 10$\sqrt{3}$米 |
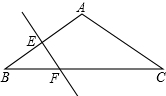 如图:△ABC中,AB=AC.∠BAC=120°,EF垂直平分AB,EF=2,求AB与BC的长.
如图:△ABC中,AB=AC.∠BAC=120°,EF垂直平分AB,EF=2,求AB与BC的长.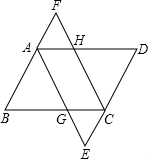 如图,在?ABCD中,E,F分别是DC,BA延长线上的点,且AE∥CF,AE,CF分别交BC,AD于点G,H,求证:EG=FH.
如图,在?ABCD中,E,F分别是DC,BA延长线上的点,且AE∥CF,AE,CF分别交BC,AD于点G,H,求证:EG=FH. 如图,二次函数y=-x2-(2m+2)x-m2-4m+3(m为非负整数)与x轴交于A、B两点,与y轴交于C点.
如图,二次函数y=-x2-(2m+2)x-m2-4m+3(m为非负整数)与x轴交于A、B两点,与y轴交于C点. 已知:如图,∠1=∠3,∠E=∠C,AD=AB,求证:BC=DE.
已知:如图,∠1=∠3,∠E=∠C,AD=AB,求证:BC=DE.