某商场的老板销售一种商品.他要以不低于进价l5%的价格才能出售.但为了获得更多利润.他以高出进价80%的价格标价．若这种商品标价为360元.你最多讲多少价时商店老板才能出售( )A．120元B．130元C．140元D．150元题目和参考答案——青夏教育精英家教网—

题目内容

2．某商场的老板销售一种商品，他要以不低于进价l5%的价格才能出售，但为了获得更多利润，他以高出进价80%的价格标价．若这种商品标价为360元，你最多讲多少价（降价多少元）时商店老板才能出售（　　）

A．

120元

B．

130元

C．

140元

D．

150元

分析设这件商品的进价为x，根据题意可得高出进价80%的价格标价为360元，列出方程，求出x的值，然后再求出最低出售价，用标价-最低出售价即可求得结论．

解答解：设这件商品的进价为x．
据题意可得：（1+80%）•x=360，
解得：x=200．
盈利的最低价格为200×（1+15%）=230，
故商店老板最多会降价360-230=130（元）．
故选：B．

点评本题考查一元一次方程的应用，将现实生活中的事件与数学思想联系起来，读懂题列出方程即可求解．

练习册系列答案

提分百分百检测卷单元期末测试卷系列答案

相关题目

17．$\sqrt{5}$，π，-4，0这四个数中，最大的数是π．

13．“垃圾分一分，环境美十分”．如果要了解人们进行垃圾分类的情况，则最合适的调查方式是（　　）

	A．	普查		B．	抽样调查
	C．	在社会上随机调查		D．	在学校里随机调查

10．

如图，△ABC是⊙O的内接三角形，∠OAB=35°，则∠ACB的度数为（　　）

17．对参加某次野外训练的中学生的年龄（单位：岁）进行统计，结果如表：

年龄	14	15	16	17	18
人数	5	6	6	7	2

则这些学生年龄的众数和中位数分别是（　　）

7．（1）解方程：x²-4x-5=0；
（2）解不等式组$\left\{\begin{array}{l}{2-x≤0}\\{2x-3＜\frac{1}{2}（x+3）}\end{array}\right.$．

14．下列函数中，当x＜0时，y随x的增大而增大的是（　　）

11．

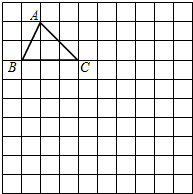如图，在10×10正方形网格中，每个小正方形的边长均为1个单位．
（1）将△ABC向下平移4个单位，得到△A′B′C′；
（2）把△A′B′C′绕点C′顺时针旋转90°，得到△A″B″C″，请你画出△A′B′C′和△A″B″C″（不要求写画法）；
（3）点B经过（1），（2）两次变换的路径长．

12．（1）计算：$\sqrt{12}+{（\frac{1}{2}）^{-2}}-4cos{30°}$；
（2）化简：$\frac{{{a^2}-4}}{{{a^2}+4a}}÷\frac{a-2}{a}$．

试题分类