题目内容
11.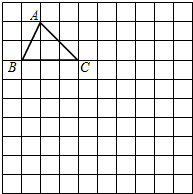 如图,在10×10正方形网格中,每个小正方形的边长均为1个单位.
如图,在10×10正方形网格中,每个小正方形的边长均为1个单位.(1)将△ABC向下平移4个单位,得到△A′B′C′;
(2)把△A′B′C′绕点C′顺时针旋转90°,得到△A″B″C″,请你画出△A′B′C′和△A″B″C″(不要求写画法);
(3)点B经过(1),(2)两次变换的路径长.
分析 (1)由平移的性质容易得到△A′B′C′;
(2)由平移的性质和旋转的性质容易画出图形;
(3)由弧长公式求出$\widehat{B′B″}$的长,点B经过(1),(2)两次变换的路径长=BB′+$\widehat{B′B″}$的长,即可得出结果.
解答 解:(1)将△ABC向下平移4个单位,得到△A′B′C′,如图1所示: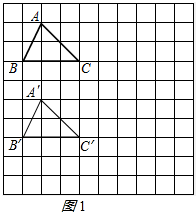
(2)把△A′B′C′绕点C′顺时针旋转90°,得到△A″B″C″,
如图2所示: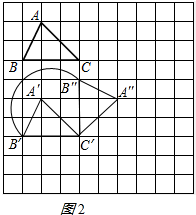
(3)根据题意得:BB′=4,B′C′=3,
$\widehat{B′B″}$的长=$\frac{90π×3}{180}$=$\frac{3π}{2}$,
故点B经过(1),(2)两次变换的路径长=BB′+$\widehat{B′B″}$的长=4+$\frac{3π}{2}$.
点评 本题考查了作图-平移变换、作图-旋转变换、弧长公式;熟练掌握平移和旋转的性质,并能进行作图与计算是解决问题的关键.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
2.某商场的老板销售一种商品,他要以不低于进价l5%的价格才能出售,但为了获得更多利润,他以高出进价80%的价格标价.若这种商品标价为360元,你最多讲多少价(降价多少元)时商店老板才能出售( )
| A. | 120元 | B. | 130元 | C. | 140元 | D. | 150元 |
1.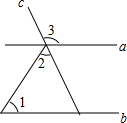 如图,直线a、b被直线c所截,若a∥b,∠1=50°,∠2=65°,则∠3的度数为( )
如图,直线a、b被直线c所截,若a∥b,∠1=50°,∠2=65°,则∠3的度数为( )
 如图,直线a、b被直线c所截,若a∥b,∠1=50°,∠2=65°,则∠3的度数为( )
如图,直线a、b被直线c所截,若a∥b,∠1=50°,∠2=65°,则∠3的度数为( )| A. | 110° | B. | 115° | C. | 120° | D. | 130° |
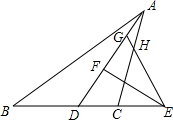 如图,在△ABC中,2AB=3AC,AD为△BAC的角平分线,点H在线段AC上,且CH=2AH,E为BC延长线上的一点,连接EH并延长交AD于点G,使EG=ED,过点E作EF⊥AD于点F,则AG:FG=4:7.
如图,在△ABC中,2AB=3AC,AD为△BAC的角平分线,点H在线段AC上,且CH=2AH,E为BC延长线上的一点,连接EH并延长交AD于点G,使EG=ED,过点E作EF⊥AD于点F,则AG:FG=4:7.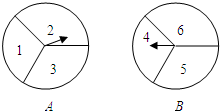 如图所示.有两个自由转动的均匀转盘A,B,都被分成了3等份,
如图所示.有两个自由转动的均匀转盘A,B,都被分成了3等份,