题目内容
7.(1)解方程:x2-4x-5=0;(2)解不等式组$\left\{\begin{array}{l}{2-x≤0}\\{2x-3<\frac{1}{2}(x+3)}\end{array}\right.$.
分析 (1)利用因式分解法解方程;
(2)分别解两个不等式得到x≥2和x<3,然后根据大于小的小于大的取中间确定不等式组的解集.
解答 解:(1)(x+1)(x-5)=0,
x+1=0或x-5=0,
所以x1=-1,x2=5;
(2)$\left\{\begin{array}{l}{2-x≤0①}\\{2x-3<\frac{1}{2}(x+3)②}\end{array}\right.$
解不等式①得x≥2,
解不等式②得x<3,
所以原不等式组的解集是2≤x<3.
点评 本题考查了解一元二次方程-因式分解法:先把方程的右边化为0,再把左边通过因式分解化为两个一次因式的积的形式,那么这两个因式的值就都有可能为0,这就能得到两个一元一次方程的解,这样也就把原方程进行了降次,把解一元二次方程转化为解一元一次方程的问题了(数学转化思想).也考查了解一元一次不等式组.

练习册系列答案
相关题目
18.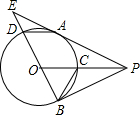 如图,P为⊙O外一点,PA、PB分别切⊙O于A、B两点,OP交⊙O于点C,连接BO并延长交⊙O于点D,交PA的延长线于点E,连接AD、BC.下列结论:①AD∥PO;②△ADE∽△PCB;③tan∠EAD=$\frac{ED}{EA}$;④BD2=2AD•OP.其中一定正确的是( )
如图,P为⊙O外一点,PA、PB分别切⊙O于A、B两点,OP交⊙O于点C,连接BO并延长交⊙O于点D,交PA的延长线于点E,连接AD、BC.下列结论:①AD∥PO;②△ADE∽△PCB;③tan∠EAD=$\frac{ED}{EA}$;④BD2=2AD•OP.其中一定正确的是( )
 如图,P为⊙O外一点,PA、PB分别切⊙O于A、B两点,OP交⊙O于点C,连接BO并延长交⊙O于点D,交PA的延长线于点E,连接AD、BC.下列结论:①AD∥PO;②△ADE∽△PCB;③tan∠EAD=$\frac{ED}{EA}$;④BD2=2AD•OP.其中一定正确的是( )
如图,P为⊙O外一点,PA、PB分别切⊙O于A、B两点,OP交⊙O于点C,连接BO并延长交⊙O于点D,交PA的延长线于点E,连接AD、BC.下列结论:①AD∥PO;②△ADE∽△PCB;③tan∠EAD=$\frac{ED}{EA}$;④BD2=2AD•OP.其中一定正确的是( )| A. | ①③④ | B. | ②④ | C. | ①②③ | D. | ①②③④ |
2.某商场的老板销售一种商品,他要以不低于进价l5%的价格才能出售,但为了获得更多利润,他以高出进价80%的价格标价.若这种商品标价为360元,你最多讲多少价(降价多少元)时商店老板才能出售( )
| A. | 120元 | B. | 130元 | C. | 140元 | D. | 150元 |
12.下列运算中,正确的运算是( )
| A. | a3+a3=a6 | B. | $\sqrt{9}$-$\sqrt{5}$=$\sqrt{4}$ | C. | $\sqrt{(-3)^{2}}$=3 | D. | (a-b)2=a2-b2 |
17.下列各数中,最大的数是( )
| A. | -2 | B. | 0 | C. | $\sqrt{2}$ | D. | 1 |
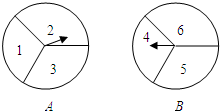 如图所示.有两个自由转动的均匀转盘A,B,都被分成了3等份,
如图所示.有两个自由转动的均匀转盘A,B,都被分成了3等份,