题目内容
12.(1)计算:$\sqrt{12}+{(\frac{1}{2})^{-2}}-4cos{30°}$;(2)化简:$\frac{{{a^2}-4}}{{{a^2}+4a}}÷\frac{a-2}{a}$.
分析 (1)原式第一项化为最简二次根式,第二项利用负整数指数幂法则计算,第三项利用特殊角的三角函数值计算即可得到结果;
(2)原式利用除法法则变形,约分即可得到结果.
解答 解:(1)原式=2$\sqrt{3}$+4-4×$\frac{\sqrt{3}}{2}$
=4;
(2)原式=$\frac{(a+2)(a-2)}{a(a+4)}$•$\frac{a}{a-2}$
=$\frac{a+2}{a+4}$.
点评 此题考查了实数的运算,以及分式的乘除法,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
2.某商场的老板销售一种商品,他要以不低于进价l5%的价格才能出售,但为了获得更多利润,他以高出进价80%的价格标价.若这种商品标价为360元,你最多讲多少价(降价多少元)时商店老板才能出售( )
| A. | 120元 | B. | 130元 | C. | 140元 | D. | 150元 |
17.下列各数中,最大的数是( )
| A. | -2 | B. | 0 | C. | $\sqrt{2}$ | D. | 1 |
1.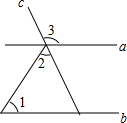 如图,直线a、b被直线c所截,若a∥b,∠1=50°,∠2=65°,则∠3的度数为( )
如图,直线a、b被直线c所截,若a∥b,∠1=50°,∠2=65°,则∠3的度数为( )
 如图,直线a、b被直线c所截,若a∥b,∠1=50°,∠2=65°,则∠3的度数为( )
如图,直线a、b被直线c所截,若a∥b,∠1=50°,∠2=65°,则∠3的度数为( )| A. | 110° | B. | 115° | C. | 120° | D. | 130° |