题目内容
1.已知$\frac{x}{3}=\frac{y}{1}=\frac{z}{2}$,求代数式$\frac{2{x}^{2}-2{y}^{2}+5{z}^{2}}{xy+yz+xz}$的值.分析 先令$\frac{x}{3}$=$\frac{y}{1}$=$\frac{z}{2}$=k,故x=3k,y=k,z=2k,再代入代数式进行计算即可.
解答 解:令$\frac{x}{3}$=$\frac{y}{1}$=$\frac{z}{2}$=k,故x=3k,y=k,z=2k,
故原式=$\frac{18{k}^{2}-2{k}^{2}+20{k}^{2}}{3k•k+k•2k+3k•2k}$
=$\frac{18{k}^{2}-2{k}^{2}+20{k}^{2}}{3{k}^{2}+2{k}^{2}+6{k}^{2}}$
=$\frac{36{k}^{2}}{11{k}^{2}}$
=$\frac{36}{11}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
16.一个正多边形中,每个外角等于它相邻内角的$\frac{2}{3}$,这个多边形的每个外角是( )
| A. | 15° | B. | 45° | C. | 36° | D. | 72° |
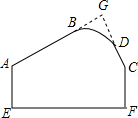 如图所示的模板,按规定AB,CD的延长线交成80°的角,因交点不在板上,测量后质检员测得∠BAE=122°,∠DCF=155°,如果你是质检员,如何知道模板是否合格?为什么?
如图所示的模板,按规定AB,CD的延长线交成80°的角,因交点不在板上,测量后质检员测得∠BAE=122°,∠DCF=155°,如果你是质检员,如何知道模板是否合格?为什么?