题目内容
6.若不等式|x+1|+|x-3|≤a有解,则a的取值范围是a≥4.分析 根据x+1和x+3的取值范围分别讨论不等式的解,从而最终确定a的值
解答 解:当x≤-1时,|x+1|+|x-3|=-x-1-x+3=-2x+2≥4,
当-1<x<3时,|x+1|+|x-3|=x+1-x+3=4,
当x≥3时,|x+1|+|x-3|=x+1+x-3=2x-2>4.
则a的范围是:a≥4.
故答案是:a≥4.
点评 本题考查了初中范围内的两个非负数,利用非负数的性质转化为解方程,这是考试中经常出现的题目类型.涉及到绝对值、不等式的解法等知识点.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案
相关题目
17.下列四组线段中,可以构成直角三角形的是( )
| A. | 2,5,7 | B. | 4,5,6 | C. | $\sqrt{2}$,$\sqrt{3}$,$\sqrt{5}$ | D. | 32,42,52 |
11.下列实例属于平移的是( )
| A. | 分针的运行 | B. | 转动的摩天轮 | C. | 直线行驶的火车 | D. | 地球自转 |
 如图所示,在△ABC中,中线BD、CE交于O,F、G分别是OB、OC的中点,求证:EG、FD互相平分.
如图所示,在△ABC中,中线BD、CE交于O,F、G分别是OB、OC的中点,求证:EG、FD互相平分.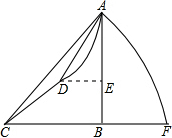 小明在山脚C处测得山顶A的仰角为45°,他沿坡角为37°的斜坡前进200米到达D处,测得山顶A的仰角为53°,求山高AB(A、B、C、D、E、F在一个平面内)参考数据:sin37°=cos53°≈$\frac{3}{5}$,cos37°=sin53°≈$\frac{4}{5}$,tan53°≈$\frac{4}{3}$.
小明在山脚C处测得山顶A的仰角为45°,他沿坡角为37°的斜坡前进200米到达D处,测得山顶A的仰角为53°,求山高AB(A、B、C、D、E、F在一个平面内)参考数据:sin37°=cos53°≈$\frac{3}{5}$,cos37°=sin53°≈$\frac{4}{5}$,tan53°≈$\frac{4}{3}$.