题目内容
半径为R的⊙O中,弦AB=2R,弦CD=R,若两弦的弦心距分别为OE、OF,则OE:OF( )
| A、2:1 | B、3:2 |
| C、2:3 | D、0 |
考点:垂径定理,勾股定理
专题:
分析:先根据弦AB=2R可知AB是⊙O的直径,故可得出OE=0,由此可得出结论.
解答:解:∵半径为R的⊙O中,弦AB=2R,
∴OE=0,
∴OE:OF=0.
故选D.
∴OE=0,
∴OE:OF=0.
故选D.
点评:本题考查的是垂径定理,熟知弦长等于半径的2倍的弦是直径是解答此题的关键.

练习册系列答案
相关题目
李华把向东移动记作“+”,向西移动记作“-”,下列说法不正确的是( )
| A、-5米表示向西移动了5米 |
| B、+5米表示向东移动了5米 |
| C、向东移动-5米表示向西移动-5米 |
| D、向西移动5米,也可记作向东移动-5米 |
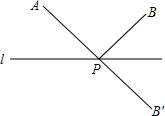 如图,点A、B在直线l的同侧,点B′是B点关于l的对称点,AB′交l于点P.
如图,点A、B在直线l的同侧,点B′是B点关于l的对称点,AB′交l于点P.