题目内容
4.计算下列各题:(1)$\frac{\sqrt{12}+\sqrt{3}}{\sqrt{3}}-\sqrt{\frac{1}{3}}×\sqrt{12}+(-2)^{-2}$$-(\sqrt{3}-1)^{0}+(-1)^{2014}$;
(2)$\frac{sin30°}{sin60°-cos45°}-\sqrt{(1-tan60°)^{2}}-tan45°$.
分析 (1)原式利用二次根式乘除法,零指数幂、负整数指数幂法则,以及乘方的意义计算即可得到结果;
(2)原式利用特殊角的三角函数值及二次根式性质计算即可得到结果.
解答 解:(1)原式=2+1-2+$\frac{1}{4}$-1+1=1$\frac{1}{4}$;
(2)原式=$\frac{\frac{1}{2}}{\frac{\sqrt{3}}{2}-\frac{\sqrt{2}}{2}}$-$\sqrt{3}$+1-1=$\sqrt{3}$+$\sqrt{2}$-$\sqrt{3}$+1-1=$\sqrt{2}$.
点评 此题考查了实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
15. 如图所示,平行四边形ABCD的对角线相交于点O,点E在边BC的延长线上,且OE=OB,OE交CD于点H,连接DE.
如图所示,平行四边形ABCD的对角线相交于点O,点E在边BC的延长线上,且OE=OB,OE交CD于点H,连接DE.
(1)求证:DE⊥BE;
(2)如果OE⊥CD,CE=3,DE=4,求BD的长度.
 如图所示,平行四边形ABCD的对角线相交于点O,点E在边BC的延长线上,且OE=OB,OE交CD于点H,连接DE.
如图所示,平行四边形ABCD的对角线相交于点O,点E在边BC的延长线上,且OE=OB,OE交CD于点H,连接DE.(1)求证:DE⊥BE;
(2)如果OE⊥CD,CE=3,DE=4,求BD的长度.
9.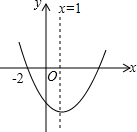 如图所示的抛物线是二次函数y=ax2+bx+c(a≠0)的图象,则下列说法错误的是( )
如图所示的抛物线是二次函数y=ax2+bx+c(a≠0)的图象,则下列说法错误的是( )
 如图所示的抛物线是二次函数y=ax2+bx+c(a≠0)的图象,则下列说法错误的是( )
如图所示的抛物线是二次函数y=ax2+bx+c(a≠0)的图象,则下列说法错误的是( )| A. | abc>0 | B. | 当x<1时,y随x的增大而减小 | ||
| C. | a-b+c>0 | D. | 当y>0时,x<-2或x>4 |
13.已知一粒大米的质量约为0.000021kg,这个数用科学记数法表示为( )
| A. | 0.21×10-4 | B. | 2.1×10-4 | C. | 2.1×10-5 | D. | 0.21×10-5 |
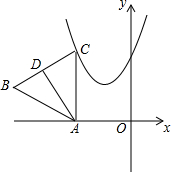 如图所示,在平面直角坐标系中,点A是x轴上一动点,过A作AC⊥x轴交抛物线y=x2+2x+2于点C,以AC为边作等边△ABC,高AD的最小值为$\frac{\sqrt{3}}{2}$.
如图所示,在平面直角坐标系中,点A是x轴上一动点,过A作AC⊥x轴交抛物线y=x2+2x+2于点C,以AC为边作等边△ABC,高AD的最小值为$\frac{\sqrt{3}}{2}$. 如图,已知AB是⊙O的直径,C是⊙O上的点,且OE⊥AC于点E,过点C作⊙O的切线,交OE的延长线于点D,交AB的延长线于点F,连接AD.(1)求证:AD是⊙O的切线;
如图,已知AB是⊙O的直径,C是⊙O上的点,且OE⊥AC于点E,过点C作⊙O的切线,交OE的延长线于点D,交AB的延长线于点F,连接AD.(1)求证:AD是⊙O的切线;
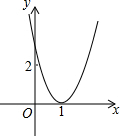 已知二次函数y=ax2+bx+c+2(a,b,c 为常数,且a≠0)的图象如图所示,其顶点坐标为(1,0).有下列结论:
已知二次函数y=ax2+bx+c+2(a,b,c 为常数,且a≠0)的图象如图所示,其顶点坐标为(1,0).有下列结论: