题目内容
6.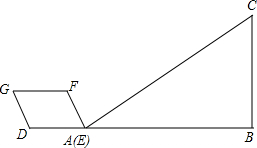 平行四边形DEFG和Rt△ABC如图放置在同一直线上,点E与点A重合,AB=9,DE=3,DG=2,∠G=∠C=60°,∠B=90°.平行四边形DEFG从如图所示状态开始向右沿AB方向以每秒1个单位的速度平移,设运动的时间为t,直到点E与点B重合为止:
平行四边形DEFG和Rt△ABC如图放置在同一直线上,点E与点A重合,AB=9,DE=3,DG=2,∠G=∠C=60°,∠B=90°.平行四边形DEFG从如图所示状态开始向右沿AB方向以每秒1个单位的速度平移,设运动的时间为t,直到点E与点B重合为止:(1)?线段EG的长度为$\sqrt{19}$;当t=4秒时,点F恰好运动到AC上;
(2)若平行四边形DEFG与Rt△ABC重叠部分的面积为S,直接写出整个运动过程中S与t之间的函数关系式,并写出相应自变量t的取值范围;
(3)在整个平移过程中,是否存在某一时刻,使以A、C、G为顶点的三角形是等腰三角形?若存在,求出此时t的值;若不存在,请说明理由.
分析 (1)如图连接AG,延长GF交AC于M,交BC于N,作AH⊥FM于H,在RT△AFH中求出FH,在RT△AFM中求出FM,即可解决问题.
(2)分四种情形讨论①当0<t≤3时,如图2中,②3<t≤4时,如图3中,③当4<t≤7时,如图4中,④当7<t≤9时,分别求解即可.
(3)①如图5中,当CG′=CE=6$\sqrt{3}$时,②如图6中,当G′C=G′A时,延长D′G′交AC于K,分别求解即可.
解答 解:(1)如图连接AG,延长GF交AC于M,交BC于N,作AH⊥FM于H.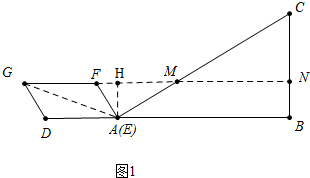
∵四边形DEFG是平行四边形,
∴DG∥AF,
∴∠AFH=∠DGH=60°,∵∠AHF=90°,AF=2,
∴FH=1,AH=$\sqrt{3}$,
∴EG=$\sqrt{G{H}^{2}+A{H}^{2}}$=$\sqrt{{4}^{2}+(\sqrt{3})^{2}}$=$\sqrt{19}$,
∵∠DGF=∠DAF=60°,∠BAC=30°,
∴∠FAM=90°,
∴FM=2AF=4,
∴t=4时点F恰好运动到AC上.
故答案分别为$\sqrt{19}$,4秒.
(2)①当0<t≤3时,如图2中,
∵∠AKE′=∠FAM=90°,∠KAE′=30°,AE′=t,
∴KE′=$\frac{1}{2}$t,AK=$\frac{\sqrt{3}}{2}$t,
∴S=$\frac{1}{2}$•AK•KE′=$\frac{\sqrt{3}}{8}$t2,
②3<t≤4时,如图3中,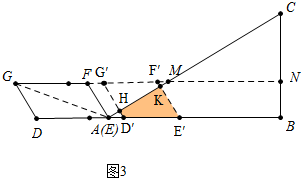
S=S四边形HKE′D′=$\frac{\sqrt{3}}{8}$t2-$\frac{\sqrt{3}}{8}$(t-3)2=$\frac{3\sqrt{3}}{4}$t-$\frac{9\sqrt{3}}{8}$.
③当4<t≤7时,如图4中,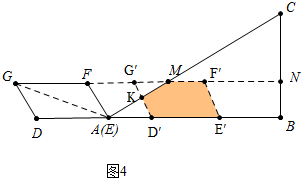
S=S平行四边形E′F′G′D′-S△KMG′=3$\sqrt{3}$-$\frac{\sqrt{3}}{4}$($\frac{7-t}{2}$)2=-$\frac{\sqrt{3}}{8}$t2+$\frac{7\sqrt{3}}{4}$t-$\frac{25\sqrt{3}}{8}$.
④当7<t≤9时,重叠部分就是平行四边形的面积,S=3$\sqrt{3}$.
综上所述S=$\left\{\begin{array}{l}{\frac{\sqrt{3}}{8}{t}^{2}}&{(0<t≤3)}\\{\frac{3\sqrt{3}}{4}t-\frac{9\sqrt{3}}{8}}&{(3<t≤4)}\\{-\frac{\sqrt{3}}{8}{t}^{2}+\frac{7\sqrt{3}}{4}t-\frac{25\sqrt{3}}{8}}&{(4<t≤7)}\\{3\sqrt{3}}&{(7<t≤9)}\end{array}\right.$,
(3)①如图5中,当CG′=CE=6$\sqrt{3}$时,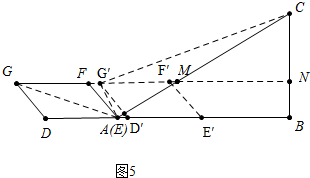
在RT△G′CN中,G′N=$\sqrt{CG{′}^{2}-C{N}^{2}}$=$\sqrt{(6\sqrt{3})^{2}-(2\sqrt{3})^{2}}$=4$\sqrt{6}$,
∴GG′=GN-G′N=13-4$\sqrt{6}$.
∴t=13-4$\sqrt{6}$.
②如图6中,当G′C=G′A时,延长D′G′交AC于K,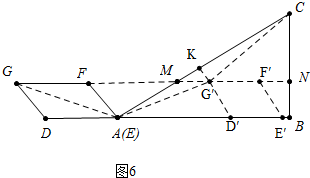
在RT△KMG′中,∵∠MKG′=90°,MK=$\sqrt{3}$,∠KMG′=30°,
∴MG′=2,
∴GG′=GF+FM+MG′=9,
∴t=9,
综上所述t=13-4$\sqrt{6}$或9秒时,使得A、C、G为顶点的三角形是等腰三角形.
点评 本题考查四边形综合题、平行四边形的性质、勾股定理、等腰三角形定义等知识,解题的关键是正确画出图形,学会分类讨论,属于中考压轴题.

| A. | 8的立方根是2 | B. | 0的立方根是0 | ||
| C. | 立方根是它本身的数只有1 | D. | a3的立方根是a |
| A. | 中位数就是一组数据中最中间的一个数 | |
| B. | 7,8,8,9,9,10这组数据的众数是8 | |
| C. | 一组数据2,4,x,2,4,7的众数是2,则这组数据的平均数是3.5,中位数是3 | |
| D. | 一组数据的方差是这组数据的极差的平方 |
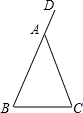 如图,在△ABC中,AB=AC,D是BA延长线上的点,现要利用尺规作图过点A作BC的平行线,下列作法不能达到目的是( )
如图,在△ABC中,AB=AC,D是BA延长线上的点,现要利用尺规作图过点A作BC的平行线,下列作法不能达到目的是( )| A. | 以A点为圆心,以AD长为半径画弧,交AC与点E;再分别以D,E为圆心,再以适当长度为半径画弧,使两弧交于点P;连接AP,则AP为所求直线 | |
| B. | 取AC中点E(作法略),作射线BE,再以E点为圆心,以BE长为半径画弧,交射线BE于另一点P;连接AP,则AP为所求直线 | |
| C. | 作∠B的角平分线(作法略)BM,再以以A点为圆心,以AB长为半径画弧,交射线BM于点P,连接AP,则AP为所求直线 | |
| D. | 将BC向上平移m个单位,让m等于A点到BC的距离,则平移后的线段为所求 |