题目内容
8. 已知:如图,等边三角形△ABC的周长为3,D为AB的中点,E在CB的延长线上,且BE=BD,连接DE.求:DE的长.
已知:如图,等边三角形△ABC的周长为3,D为AB的中点,E在CB的延长线上,且BE=BD,连接DE.求:DE的长.
分析 根据等边三角形的性质得到AB=AC=BC=1,∠A=∠ABC=∠ACB=60°,CD⊥AB,AD=$\frac{1}{3}$AB=$\frac{1}{2}$,根据勾股定理得到CD=$\sqrt{A{C}^{2}-A{D}^{2}}$=$\frac{\sqrt{3}}{2}$,于是得到结论.
解答 解:∵△ABC是等边三角形,且周长为3,
∴AB=AC=BC=1,∠A=∠ABC=∠ACB=60°,
∵D为AB的中点,
∴CD⊥AB,AD=$\frac{1}{3}$AB=$\frac{1}{2}$,
∠DCA=∠DCB=$\frac{1}{2}∠$ACB=30°,
∴CD=$\sqrt{A{C}^{2}-A{D}^{2}}$=$\frac{\sqrt{3}}{2}$,
∵BE=BD,∠ABC=∠E+∠BDE,
∴∠E=∠BDE=$\frac{1}{2}∠$ACB=30°=∠DCB,
∴CD=DE=$\frac{\sqrt{3}}{2}$.
点评 本题考查了等边三角形的性质.勾股定理,熟练掌握等边三角形的性质是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.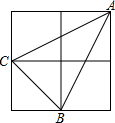 图中的大正方形是由4个小正方形组成的,小正方形边长为1,连接小正方形的三个顶点,得到△ABC,则AC边上的高为( )
图中的大正方形是由4个小正方形组成的,小正方形边长为1,连接小正方形的三个顶点,得到△ABC,则AC边上的高为( )
 图中的大正方形是由4个小正方形组成的,小正方形边长为1,连接小正方形的三个顶点,得到△ABC,则AC边上的高为( )
图中的大正方形是由4个小正方形组成的,小正方形边长为1,连接小正方形的三个顶点,得到△ABC,则AC边上的高为( )| A. | $\frac{3\sqrt{5}}{5}$ | B. | $\frac{4\sqrt{5}}{5}$ | C. | $\frac{5\sqrt{5}}{10}$ | D. | $\frac{3\sqrt{2}}{2}$ |
13.研究发现,学生对概念的接受能力y与提出概念所用的时间x(分钟)之间有如下关系:(0≤x≤30)
根据以上信息,回答下列问题:
(1)表中描述的变化过程中,自变量是什么?因变量是什么?
(2)当提出概念所用的时间为10分钟时,学生的接受能力约是多少?
(3)当提出概念所用的时间为多少分钟时,学生的接受能力最强?
(4)在什么时间范围内,学生的接受能力在逐渐增强?什么时间范围内,学生的接受能力在逐渐增强减弱?
| 提出概念所用的时间x(分钟) | 2 | 5 | 7 | 10 | 12 | 13 | 14 | 17 | 20 |
| 对概念的接受能力y | 47.8 | 53.5 | 56.3 | 59 | 59.8 | 59.9 | 59.8 | 58.3 | 55 |
(1)表中描述的变化过程中,自变量是什么?因变量是什么?
(2)当提出概念所用的时间为10分钟时,学生的接受能力约是多少?
(3)当提出概念所用的时间为多少分钟时,学生的接受能力最强?
(4)在什么时间范围内,学生的接受能力在逐渐增强?什么时间范围内,学生的接受能力在逐渐增强减弱?
 如图,边长为2菱形ABCD中,∠DAB=60°,连接对角线AC,以AC为边作第二个菱形ACC1D1,使∠D1AC=60°;连接AC1,再以AC1为边作第三个菱形AC1C2D2,使∠D2AC1=60°;…,按此规律所作的第4个菱形的边长为6$\sqrt{3}$.
如图,边长为2菱形ABCD中,∠DAB=60°,连接对角线AC,以AC为边作第二个菱形ACC1D1,使∠D1AC=60°;连接AC1,再以AC1为边作第三个菱形AC1C2D2,使∠D2AC1=60°;…,按此规律所作的第4个菱形的边长为6$\sqrt{3}$.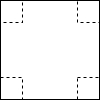 如图,把一边长为xcm的正方形纸板的四个角各剪去一个边长为ycm的小正方形,然后把它折成一个无盖纸盒.
如图,把一边长为xcm的正方形纸板的四个角各剪去一个边长为ycm的小正方形,然后把它折成一个无盖纸盒.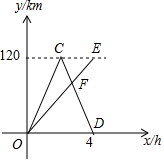 A,B两地相距120km,甲、乙两车同时从A地出发驶向B地,甲车到达B地后立即按原速返回.如图是它们离A地的距离y(km)与行驶时间x(h)之间的函数图象.
A,B两地相距120km,甲、乙两车同时从A地出发驶向B地,甲车到达B地后立即按原速返回.如图是它们离A地的距离y(km)与行驶时间x(h)之间的函数图象.