题目内容
18. 如图,边长为2菱形ABCD中,∠DAB=60°,连接对角线AC,以AC为边作第二个菱形ACC1D1,使∠D1AC=60°;连接AC1,再以AC1为边作第三个菱形AC1C2D2,使∠D2AC1=60°;…,按此规律所作的第4个菱形的边长为6$\sqrt{3}$.
如图,边长为2菱形ABCD中,∠DAB=60°,连接对角线AC,以AC为边作第二个菱形ACC1D1,使∠D1AC=60°;连接AC1,再以AC1为边作第三个菱形AC1C2D2,使∠D2AC1=60°;…,按此规律所作的第4个菱形的边长为6$\sqrt{3}$.
分析 根据已知和菱形的性质可分别求得AC,AC1,AC2的长,从而可发现规律,根据规律不难求得第4个菱形的边长.
解答  解:连接DB,
解:连接DB,
∵四边形ABCD是菱形,
∴AD=AB.AC⊥DB,
∵∠DAB=60°,
∴△ADB是等边三角形,
∴DB=AD=2,
∴BM=1,
∴AM=$\sqrt{{2}^{2}-{1}^{2}}$=$\sqrt{3}$,
∴AC=2AM=2$\sqrt{3}$,
同理可得AC1=$\sqrt{3}$AC=6,AC2=$\sqrt{3}$AC1=6$\sqrt{3}$.
故答案为:6$\sqrt{3}$.
点评 本题考查了菱形的性质,勾股定理,等边三角形的性质和判定的应用,解此题的关键是能根据求出的结果得出规律.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
 如图,△ABC 中,∠C=90°,AC=4,BC=8,以AB为边向外作正方形ABDE,若此正方形中心为点O,则点C和点O之间的距离为6$\sqrt{2}$.
如图,△ABC 中,∠C=90°,AC=4,BC=8,以AB为边向外作正方形ABDE,若此正方形中心为点O,则点C和点O之间的距离为6$\sqrt{2}$.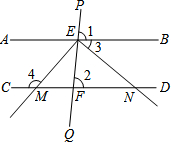 已知:如图,直线PQ分别与直线AB、CD交于点E和点F,∠1=∠2,射线EM、EN分别与直线CD交于点M、N,且EM⊥EN,∠3=40°,求∠4的度数.
已知:如图,直线PQ分别与直线AB、CD交于点E和点F,∠1=∠2,射线EM、EN分别与直线CD交于点M、N,且EM⊥EN,∠3=40°,求∠4的度数. 如图,在平行四边形ABCD中,AD=AC,∠B=65°,DE⊥AC于E,则∠EDC=25°.
如图,在平行四边形ABCD中,AD=AC,∠B=65°,DE⊥AC于E,则∠EDC=25°. 已知:如图,等边三角形△ABC的周长为3,D为AB的中点,E在CB的延长线上,且BE=BD,连接DE.求:DE的长.
已知:如图,等边三角形△ABC的周长为3,D为AB的中点,E在CB的延长线上,且BE=BD,连接DE.求:DE的长.