题目内容
13.研究发现,学生对概念的接受能力y与提出概念所用的时间x(分钟)之间有如下关系:(0≤x≤30)| 提出概念所用的时间x(分钟) | 2 | 5 | 7 | 10 | 12 | 13 | 14 | 17 | 20 |
| 对概念的接受能力y | 47.8 | 53.5 | 56.3 | 59 | 59.8 | 59.9 | 59.8 | 58.3 | 55 |
(1)表中描述的变化过程中,自变量是什么?因变量是什么?
(2)当提出概念所用的时间为10分钟时,学生的接受能力约是多少?
(3)当提出概念所用的时间为多少分钟时,学生的接受能力最强?
(4)在什么时间范围内,学生的接受能力在逐渐增强?什么时间范围内,学生的接受能力在逐渐增强减弱?
分析 (1)根据题意得出是自变量和因变量;
(2)利用图表中数据得出答案;
(3)利用图表中数据得出答案;
(4)利用图表中数据得出答案.
解答 解:(1)提出概念所用的时间x是自变量,学生对概念接受能力y是因变量;
(2)当x=10时,y=59,所以时间是10分钟时,学生的接受能力是59.
(3)当x=13时,y的值最大是59.9,所以提出概念13分钟时,学生的接受能力最强.
(4)由表中数据可知:当0<x<13时,y值逐渐增大,学生的接受能力逐步增强;
当13<x<20时,y值逐渐减小,学生的接受能力逐步减弱.
点评 此题主要考查了函数的表示方法以及常量与变量,正确利用表格中数据得出是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.已知:在△ABC中,∠C=90°,若AC+BC=14cm,AB=10cm,则Rt△ABC的面积是( )
| A. | 24cm2 | B. | 36cm2 | C. | 48cm2 | D. | 60cm2 |
2.下列说法正确的是( )
①内错角相等;②过直线外一点有且只有一条直线与已知直线平行;③相等的角是对顶角;④幂的乘方,底数不变,指数相加;⑤两个角的和为90°,则这两个角互补.
①内错角相等;②过直线外一点有且只有一条直线与已知直线平行;③相等的角是对顶角;④幂的乘方,底数不变,指数相加;⑤两个角的和为90°,则这两个角互补.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
3.已知2-$\sqrt{3}$是关于x的方程x2-4x+c=0的一个根,则方程的另一个根与c的值是( )
| A. | $\sqrt{3}$-2,-1 | B. | -6-$\sqrt{3}$,15-8$\sqrt{3}$ | C. | 2+$\sqrt{3}$,1 | D. | 2+$\sqrt{3}$,7-4$\sqrt{3}$ |
 已知:如图,等边三角形△ABC的周长为3,D为AB的中点,E在CB的延长线上,且BE=BD,连接DE.求:DE的长.
已知:如图,等边三角形△ABC的周长为3,D为AB的中点,E在CB的延长线上,且BE=BD,连接DE.求:DE的长.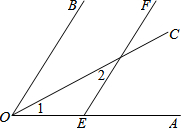 如图,OC是∠AOB的平分线,且∠1=∠2,探索EF与OB的位置关系,并说明理由.
如图,OC是∠AOB的平分线,且∠1=∠2,探索EF与OB的位置关系,并说明理由.