题目内容
5.我区某单位为响应全民健身的号召,一次性购买若干副乒乓球拍和羽毛球拍(每副乒乓球拍的价格相同,每副羽毛球拍的价格相同),若购买2副乒乓球拍和1副羽毛球拍共需540元,购买1副乒乓球拍和2副羽毛球拍共需660元,问:(1)购买1副乒乓球拍、1副羽毛球拍各需多少元?
(2)根据该单位的实际情况,需一次性购买乒乓球拍、羽毛球拍共10副,要求购买乒乓球拍、羽毛球拍的总费用不超过2500元,该单位最多可以购买多少副羽毛球拍?
分析 (1)可设购买1副乒乓球拍需x元、1副羽毛球拍需y元,根据等量关系:①购买2副乒乓球拍和1副羽毛球拍共需540元,②购买1副乒乓球拍和2副羽毛球拍共需660元,列出方程组求解即可;
(2)可设该单位购买k副羽毛球拍,则乒乓球拍为(10-k)副,根据购买乒乓球拍、羽毛球拍的总费用不超过2500元,列出不等式求解即可.
解答 解:(1)设购买1副乒乓球拍需x元、1副羽毛球拍需y元,依题意有
$\left\{\begin{array}{l}{2x+y=540}\\{x+2y=660}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=140}\\{y=260}\end{array}\right.$.
答:购买1副乒乓球拍需140元、1副羽毛球拍需260元;
(2)设该单位购买k副羽毛球拍,则乒乓球拍为(10-k)副,依题意有
260k+140(10-k)≤2500,
解得k≤$\frac{55}{6}$,
∵k为整数,
∴k最多为9.
故该单位最多可以购买9副羽毛球拍.
点评 考查了二元一次方程组的应用,一元一次不等式的应用,解决问题的关键是读懂题意,找到关键描述语,找到所求的量的等量关系和不等量关系.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
13.数【x】是表示不大于x的最大整数,如【-1.2】=-2,【2.3】=2,【1】=1,则【$\sqrt{7}$】+【-$\sqrt{5}$】+【$\sqrt{3}$】的值为( )
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
12.某房地产开发公司计划建A、B两种户型的住房共80套,A种户型每套成本和售价分别为90万元和102万元,B种户型每套成本和售价分别为60万元和70万元.设计划建A户型x套,所建户型全部售出后获得的总利润为W万元.
【思考】
(1)根据所给条件,完成下表:
(2)求W与x之间的函数解析式;
【探究】
(3)该公司所建房资金不少于5700万元,且所筹资金全部用于建房,若A户型不超过32套,则该公司有哪几种建房方案?
(4)在(3)的前提下,根据国家房地产政策,公司计划每套A户型住房的售价降低a万元(0<a≤3),B户型住房的售价不变,且预计所建的两种住房全部售出,求该公司获得最大利润的方案.
【决策】
为了适应市场需要,该公司在总套数不变的情况下,改建若干套C户型,现已知C户型每套成本110万元,售价118万元.若该公司所筹资金为6300万元且刚好用完,则当x=45套时,该公司所建房售出后获得的总利润最大.
【思考】
(1)根据所给条件,完成下表:
| A户型 | B户型 | |
| 套数 | x | 80-x |
| 利润(万元) | 12x | 10(80-x) |
【探究】
(3)该公司所建房资金不少于5700万元,且所筹资金全部用于建房,若A户型不超过32套,则该公司有哪几种建房方案?
(4)在(3)的前提下,根据国家房地产政策,公司计划每套A户型住房的售价降低a万元(0<a≤3),B户型住房的售价不变,且预计所建的两种住房全部售出,求该公司获得最大利润的方案.
【决策】
为了适应市场需要,该公司在总套数不变的情况下,改建若干套C户型,现已知C户型每套成本110万元,售价118万元.若该公司所筹资金为6300万元且刚好用完,则当x=45套时,该公司所建房售出后获得的总利润最大.
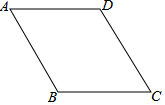 如图,在菱形ABCD中,∠ABC=120°,AB=10cm,点P是这个菱形内部或边上的一点.若以P,B,C为顶点的三角形是等腰三角形,则P,A(P,A两点不重合)两点间的最短距离为10$\sqrt{3}$-10cm.
如图,在菱形ABCD中,∠ABC=120°,AB=10cm,点P是这个菱形内部或边上的一点.若以P,B,C为顶点的三角形是等腰三角形,则P,A(P,A两点不重合)两点间的最短距离为10$\sqrt{3}$-10cm.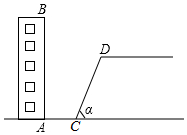 如图,某校教学楼AB后方有一斜坡,已知斜坡CD的长为12米,坡角α为60°,根据有关部门的规定,∠α≤39°时,才能避免滑坡危险,学校为了消除安全隐患,决定对斜坡CD进行改造,在保持坡脚C不动的情况下,学校至少要把坡顶D向后水平移动多少米才能保证教学楼的安全?(结果取整数)
如图,某校教学楼AB后方有一斜坡,已知斜坡CD的长为12米,坡角α为60°,根据有关部门的规定,∠α≤39°时,才能避免滑坡危险,学校为了消除安全隐患,决定对斜坡CD进行改造,在保持坡脚C不动的情况下,学校至少要把坡顶D向后水平移动多少米才能保证教学楼的安全?(结果取整数)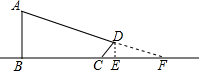 小明在某一时刻测得1m的杆子在阳光下的影子长为2m,他想测量电线杆AB的高度,但其影子恰好落在土坡的坡面CD和地面BC上,量得CD=4m,BC=10m,CD与底面成45°,求电线杆的高度.
小明在某一时刻测得1m的杆子在阳光下的影子长为2m,他想测量电线杆AB的高度,但其影子恰好落在土坡的坡面CD和地面BC上,量得CD=4m,BC=10m,CD与底面成45°,求电线杆的高度.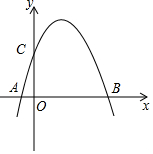 如图,已知抛物线y=ax2+bx+c(a≠0)经过A(-1,0),B(3,0),C(0,3)三点,O为坐标原点.
如图,已知抛物线y=ax2+bx+c(a≠0)经过A(-1,0),B(3,0),C(0,3)三点,O为坐标原点.