题目内容
7.将4cm长的线段分成两部分,一部分作为正方形的一条边,另一部分作为一个等腰直角三角形的斜边,则这个正方形和等腰直角三角形的面积之和的最小值为( )cm2.| A. | 1 | B. | $\frac{4}{5}$ | C. | 16 | D. | $\frac{16}{5}$ |
分析 设等腰直角三角形的斜边为x,则正方形的边长为10-x.分别用含x的式子表示两个图形的面积,再求和的表达式,运用函数性质求解.
解答 解:设等腰直角三角形的斜边为xcm,则正方形的边长为(4-x)cm.若等腰直角三角形的面积为S1,正方形面积为S2,则
S1=$\frac{1}{2}$•x•$\frac{1}{2}$x=$\frac{1}{4}$x2,S2=(4-x)2,
面积之和S=$\frac{1}{4}$x2+(4-x)2=$\frac{5}{4}$x2-8x+16.
∵$\frac{5}{4}$>0,
∴函数有最小值.
即S最小值=$\frac{4×\frac{5}{4}×16-64}{4×\frac{5}{4}}$=$\frac{16}{5}$(cm2).
故选:D.
点评 本题考查了二次函数的最值.此题的关键在数学建模思想的应用.选择合适的未知量表示面积得到函数关系式,再运用函数性质求解.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
18. 如图,在⊙O中,直径AB丄弦CD于点M,AM=18,BM=8,则CD的长为( )
如图,在⊙O中,直径AB丄弦CD于点M,AM=18,BM=8,则CD的长为( )
 如图,在⊙O中,直径AB丄弦CD于点M,AM=18,BM=8,则CD的长为( )
如图,在⊙O中,直径AB丄弦CD于点M,AM=18,BM=8,则CD的长为( )| A. | 12 | B. | 18 | C. | 20 | D. | 24 |
15.以下列长度的线段为边不能构成直角三角形的是( )
| A. | 3,4,5 | B. | 6,8,10 | C. | 5,12,13 | D. | 6,24,25 |
2.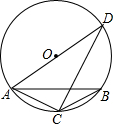 如图,AD是⊙O的直径,∠ACB=120°,$\widehat{AC}$=$\widehat{BC}$,BC=2$\sqrt{3}$,则DC的长是( )
如图,AD是⊙O的直径,∠ACB=120°,$\widehat{AC}$=$\widehat{BC}$,BC=2$\sqrt{3}$,则DC的长是( )
 如图,AD是⊙O的直径,∠ACB=120°,$\widehat{AC}$=$\widehat{BC}$,BC=2$\sqrt{3}$,则DC的长是( )
如图,AD是⊙O的直径,∠ACB=120°,$\widehat{AC}$=$\widehat{BC}$,BC=2$\sqrt{3}$,则DC的长是( )| A. | 2 | B. | 2$\sqrt{3}$ | C. | 4$\sqrt{3}$ | D. | 6 |
12.如果a-3b=6,那么代数式5-a+3b的值是( )
| A. | 11 | B. | -11 | C. | 1 | D. | -1 |
16.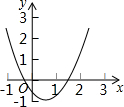 如图是二次函数y=ax2+bx+c(a≠0)在平面直角坐标系中的图象,根据图形判断①b>0;②a-b+c<0;③2a+b>0;④b2+8a>4ac中正确的是( )
如图是二次函数y=ax2+bx+c(a≠0)在平面直角坐标系中的图象,根据图形判断①b>0;②a-b+c<0;③2a+b>0;④b2+8a>4ac中正确的是( )
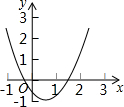 如图是二次函数y=ax2+bx+c(a≠0)在平面直角坐标系中的图象,根据图形判断①b>0;②a-b+c<0;③2a+b>0;④b2+8a>4ac中正确的是( )
如图是二次函数y=ax2+bx+c(a≠0)在平面直角坐标系中的图象,根据图形判断①b>0;②a-b+c<0;③2a+b>0;④b2+8a>4ac中正确的是( )| A. | ①② | B. | ①③ | C. | ③④ | D. | ②④ |
17.大于-3而不大于3的所有整数的和是( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
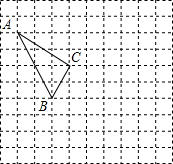 在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(-4,5),(-1,3).
在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(-4,5),(-1,3).