题目内容
17.列代数式(1)连续三个整数,中间一个是n,则三个整数的和是多少?
(2)a,b两数的平方和与a,b两数平方差的积.
(3)x,y两数和的3倍与x,y两数差的2倍的商.
分析 (1)根据相邻的2个连续整数相隔1,分别得到最小的数和最大的数,把三个数相加即可;
(2)先分别表示出a,b两数的平方和与a,b两数平方差,再两者相乘即可;
(3)先分别表示出x,y两数和的3倍和x,y两数差的2倍,再两者相除即可.
解答 解:(1)∵三个连续整数的中间的一个数是n,
∴最小的数为n-1,最大的数为n+1,
∴它们三个数的和是(n-1)+n+(n+1)=3n;
(2)∵a,b两数的平方和可表示为:a2+b2,
a,b两数平方差可表示为a2-b2,
∴a,b两数的平方和与a,b两数平方差的积可表示为:(a2+b2)(a2-b2)=a4-b4;
(3)∵x,y两数和的3倍可表示为:3(x+y),
x,y两数差的2倍克表示为:2(x-y),
∴x,y两数和的3倍与x,y两数差的2倍的商可表示为:$\frac{3(x+y)}{2(x-y)}$.
点评 此题主要考查了如何列代数式,解决问题的关键是分解题干,正确搞清题目的要求,从而列出代数式.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
5.下面四句话中,正确句子的个数是( )
(1)-5的相反数是5
(2)-5的倒数是-$\frac{1}{5}$
(3)-5与5的绝对值都是5
(4)零的相反数、倒数、绝对值都是零.
(1)-5的相反数是5
(2)-5的倒数是-$\frac{1}{5}$
(3)-5与5的绝对值都是5
(4)零的相反数、倒数、绝对值都是零.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
2.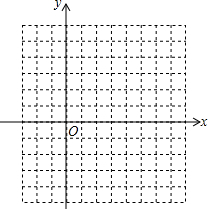 对于抛物线y=x2-4x+3.
对于抛物线y=x2-4x+3.
(1)将抛物线的解析式化为顶点式.
(2)在坐标系中利用五点法画出此抛物线.
(3)结合图象,当0<x<3时,y的取值范围-1≤y<3.
 对于抛物线y=x2-4x+3.
对于抛物线y=x2-4x+3.(1)将抛物线的解析式化为顶点式.
(2)在坐标系中利用五点法画出此抛物线.
| x | … | … | |||||
| y | … | … |
9.计算(-$\frac{1}{7}$)-3的结果是( )
| A. | -$\frac{1}{343}$ | B. | -$\frac{1}{21}$ | C. | -343 | D. | -21 |
7.将4cm长的线段分成两部分,一部分作为正方形的一条边,另一部分作为一个等腰直角三角形的斜边,则这个正方形和等腰直角三角形的面积之和的最小值为( )cm2.
| A. | 1 | B. | $\frac{4}{5}$ | C. | 16 | D. | $\frac{16}{5}$ |
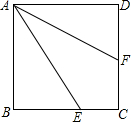 如图,已知正方形ABCD,点E在BC上,BE=2EC,点F在CD上,∠EAF=30°,求$\frac{CF}{DF}$.
如图,已知正方形ABCD,点E在BC上,BE=2EC,点F在CD上,∠EAF=30°,求$\frac{CF}{DF}$.