题目内容
6.把能表示为2个正整数的平方差的正整数,从小到大排成一列设为a1,a2…an,则a1+a2+…a100=6999.分析 根据平方差公式,可得4k=(k+1)2-(k-1)2,4k+1=(2k+1)2-(2k)2,4k+3=(2k+2)2-(2k+1)2,根据整式的加法,可得4k+(4k+1)+(4k+3)=12k+4,可得k=2,k=3,…k=33,可得答案.
解答 解:∵偶数中不是4的倍数的整数不可能是两个整数的平方差,
a1=22-12=3,a2=32-22=5,a3=42-32=7,
∴a1=3,a2=5,a3=7.
当k≥2,k为正整数,则有4k=(k+1)2-(k-1)2,
4k+1=(2k+1)2-(2k)2,
4k+3=(2k+2)2-(2k+1)2,
且4k+(4k+1)+(4k+3)=12k+4,
∴a4+a5+a6=12×2+4,
a7+a8+a9=12×3+4,
…
a97+a98+a99=12×33+4,
a100=4×34,
则a1+a2+…+a100=3+5+7+12(2+3+…+33)+4×32+4×34=6999,
故答案为:6999.
点评 本题考查了平方差公式,利用平方差公式得出k≥2,k为正整数,则有4k=(k+1)2-(k-1)2,4k+1=(2k+1)2-(2k)2,4k+3=(2k+2)2-(2k+1)2,且4k+(4k+1)+(4k+3)=12k+4是解题关键.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
1.在平面直角坐标系中,将点B(-3,2)向右平移5个单位长度,再向下平移3个单位长度后与点A(x,y)重合,则点A的坐标是( )
| A. | (2,5) | B. | (-8,5) | C. | (-8,-1) | D. | (2,-1) |




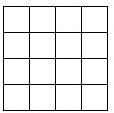 如图,将3枚相同硬币依次放入一个4×4的正方形格子中(每个正方形格子只能放1枚硬币).求所放的3枚硬币中,任意两个都不同行且不同列的概率.
如图,将3枚相同硬币依次放入一个4×4的正方形格子中(每个正方形格子只能放1枚硬币).求所放的3枚硬币中,任意两个都不同行且不同列的概率.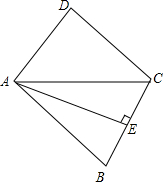 如图所示,在菱形ABCD中,AE⊥BC,E为垂足,且BE=CE,AB=2,求:
如图所示,在菱形ABCD中,AE⊥BC,E为垂足,且BE=CE,AB=2,求: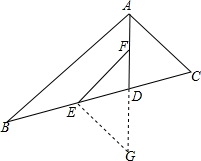 已知:AD是∠BAC的平分线,CD=DE,EF∥AB.求证:EF=AC.
已知:AD是∠BAC的平分线,CD=DE,EF∥AB.求证:EF=AC. 以等腰△ABC的腰AB为直径作半圆,设圆心为点O,半圆与另一腰交于点D,与底BC交于点E,取线段CD的中点F,连接EF.
以等腰△ABC的腰AB为直径作半圆,设圆心为点O,半圆与另一腰交于点D,与底BC交于点E,取线段CD的中点F,连接EF.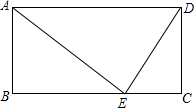 已知:如图,在矩形ABCD中,E为BC上一点.若AB=12,AD=25,BE=16,求证:△ABE∽△ECD.
已知:如图,在矩形ABCD中,E为BC上一点.若AB=12,AD=25,BE=16,求证:△ABE∽△ECD.