题目内容
13.反比例函数y=$\frac{k}{x}$的图象过点P(a,b),其中a、b是一元二次方程-x2+10x+4=0的两个根,则k=-4.分析 先利用根与系数的关系得到ab=-4,然后根据反比例函数图象上点的坐标特征求k的值.
解答 解:∵a、b是一元二次方程-x2+10x+4=0的两个根,
∴ab=-4,
∵反比例函数y=$\frac{k}{x}$的图象过点P(a,b),
∴k=ab=-4.
故答案为-4.
点评 本题考查了反比例函数图象上点的坐标特征:反比例函数y=$\frac{k}{x}$(k为常数,k≠0)的图象是双曲线,图象上的点(x,y)的横纵坐标的积是定值k,即xy=k.也考查了根与系数的关系.

练习册系列答案
相关题目
8.2的平方根是( )
| A. | ±$\sqrt{2}$ | B. | $\sqrt{2}$ | C. | ±1.414 | D. | 4 |
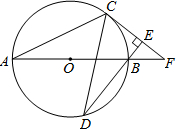 如图,AB为⊙O的直径,C,D为⊙O上不同于A,B的两点,过点C作⊙O的切线CF交直线AB于点F,直线DB⊥CF于点E.
如图,AB为⊙O的直径,C,D为⊙O上不同于A,B的两点,过点C作⊙O的切线CF交直线AB于点F,直线DB⊥CF于点E.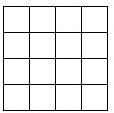 如图,将3枚相同硬币依次放入一个4×4的正方形格子中(每个正方形格子只能放1枚硬币).求所放的3枚硬币中,任意两个都不同行且不同列的概率.
如图,将3枚相同硬币依次放入一个4×4的正方形格子中(每个正方形格子只能放1枚硬币).求所放的3枚硬币中,任意两个都不同行且不同列的概率. 如图,四边形ABCD是平行四边形,AD=30cm,AB=20cm,∠D=60°,E、F分别为AB和CD边上的两个动点,E从A向B运动,F从D向C运动,若点E的速度是1cm/秒,点F的速度是2cm/秒.
如图,四边形ABCD是平行四边形,AD=30cm,AB=20cm,∠D=60°,E、F分别为AB和CD边上的两个动点,E从A向B运动,F从D向C运动,若点E的速度是1cm/秒,点F的速度是2cm/秒.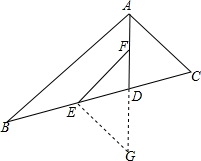 已知:AD是∠BAC的平分线,CD=DE,EF∥AB.求证:EF=AC.
已知:AD是∠BAC的平分线,CD=DE,EF∥AB.求证:EF=AC.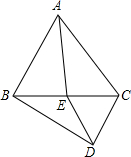 如图所示,△ABC、△DEC是等边三角形.
如图所示,△ABC、△DEC是等边三角形. 如图,己知△ABC是等腰直角三角形,AC=BC,∠ACB=90°,AE⊥EF于E,BF⊥EF于F,求证:EF=AE+BF.
如图,己知△ABC是等腰直角三角形,AC=BC,∠ACB=90°,AE⊥EF于E,BF⊥EF于F,求证:EF=AE+BF. 如图,△AOB为等腰三角形,∠ABO=90°,点A为x轴上的点,过点A作AC⊥x轴交双曲线y=$\frac{k}{x}$于C,AC=1,求k的值.
如图,△AOB为等腰三角形,∠ABO=90°,点A为x轴上的点,过点A作AC⊥x轴交双曲线y=$\frac{k}{x}$于C,AC=1,求k的值.