题目内容
14.若关于x,y的二元一次方程组$\left\{\begin{array}{l}{2x+y=3k-1}\\{x+2y=-2}\end{array}\right.$的解满足x大于3,y不大于-3,求k的取值范围.分析 先把k看作常数,解关于x,y的二元一次方程组,再根据x大于3、y不大于-3得出关于k的不等式组,解不等式组即可求出k的取值范围.
解答 解:解方程组$\left\{\begin{array}{l}{2x+y=3k-1}&{①}\\{x+2y=-2}&{②}\end{array}\right.$,
①×2,得:4x+2y=6k-2 ③,
③-②,得:3x=6k,解得:x=2k,
将x=2k代入①,得:4k+y=3k-1,解得:y=-k-1,
∵方程组的解满足x大于3,y不大于-3,
∴$\left\{\begin{array}{l}{2k>3}\\{-k-1≤-3}\end{array}\right.$
解得:k≥2.
点评 主要考查了方程组的解的定义和不等式的解法.理解方程组解的意义用含k的代数式表示出x,y,找到关于x,y的不等式并k表示出来是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.五张完全相同的卡片上,分别写上数字-3,-2,-1,2,3,现从中随机抽取一张,抽到写有负数的卡片的概率是( )
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |




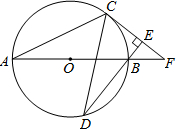 如图,AB为⊙O的直径,C,D为⊙O上不同于A,B的两点,过点C作⊙O的切线CF交直线AB于点F,直线DB⊥CF于点E.
如图,AB为⊙O的直径,C,D为⊙O上不同于A,B的两点,过点C作⊙O的切线CF交直线AB于点F,直线DB⊥CF于点E.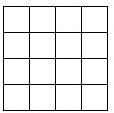 如图,将3枚相同硬币依次放入一个4×4的正方形格子中(每个正方形格子只能放1枚硬币).求所放的3枚硬币中,任意两个都不同行且不同列的概率.
如图,将3枚相同硬币依次放入一个4×4的正方形格子中(每个正方形格子只能放1枚硬币).求所放的3枚硬币中,任意两个都不同行且不同列的概率.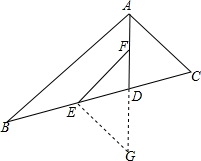 已知:AD是∠BAC的平分线,CD=DE,EF∥AB.求证:EF=AC.
已知:AD是∠BAC的平分线,CD=DE,EF∥AB.求证:EF=AC.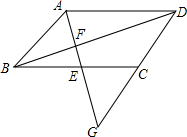 如图,直线AG过平行四边形ABCD的边BC的中点F、交对角线BD于点F,交DC的延长线于G.
如图,直线AG过平行四边形ABCD的边BC的中点F、交对角线BD于点F,交DC的延长线于G.