题目内容
10.已知y=y1+y2,y1与x成正比例,y2与x成反比例,且当x=1和x=-3时,y的值分别为-4和3.试求出y与x之间的函数关系式.分析 设y与x之间的函数关系式为y=ax+$\frac{b}{x}$,将点(1,-4)和点(-3,3)代入函数关系式中得出关于a、b的二元一次方程组,解方程组即可得出结论.
解答 解:设y与x之间的函数关系式为y=ax+$\frac{b}{x}$,
由已知得:$\left\{\begin{array}{l}{-4=a+b}\\{3=-3a-\frac{b}{3}}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-\frac{5}{8}}\\{b=-\frac{27}{8}}\end{array}\right.$.
∴y与x之间的函数关系式为y=-$\frac{5}{8}$x-$\frac{27}{8x}$(x≠0).
点评 本题考查了待定系数法求反比例函数解析式,解题的关键是将点的坐标代入函数关系式中得出关于a、b的二元一次方程组.本题属于基础题,难度不大,解决该题型题目时,将点的坐标代入函数关系式得出方程(或方程组)是关键.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
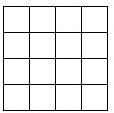 如图,将3枚相同硬币依次放入一个4×4的正方形格子中(每个正方形格子只能放1枚硬币).求所放的3枚硬币中,任意两个都不同行且不同列的概率.
如图,将3枚相同硬币依次放入一个4×4的正方形格子中(每个正方形格子只能放1枚硬币).求所放的3枚硬币中,任意两个都不同行且不同列的概率.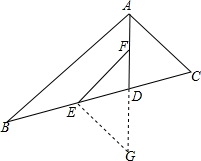 已知:AD是∠BAC的平分线,CD=DE,EF∥AB.求证:EF=AC.
已知:AD是∠BAC的平分线,CD=DE,EF∥AB.求证:EF=AC.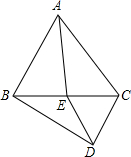 如图所示,△ABC、△DEC是等边三角形.
如图所示,△ABC、△DEC是等边三角形. 以等腰△ABC的腰AB为直径作半圆,设圆心为点O,半圆与另一腰交于点D,与底BC交于点E,取线段CD的中点F,连接EF.
以等腰△ABC的腰AB为直径作半圆,设圆心为点O,半圆与另一腰交于点D,与底BC交于点E,取线段CD的中点F,连接EF. 如图,己知△ABC是等腰直角三角形,AC=BC,∠ACB=90°,AE⊥EF于E,BF⊥EF于F,求证:EF=AE+BF.
如图,己知△ABC是等腰直角三角形,AC=BC,∠ACB=90°,AE⊥EF于E,BF⊥EF于F,求证:EF=AE+BF.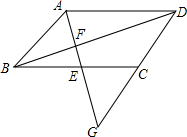 如图,直线AG过平行四边形ABCD的边BC的中点F、交对角线BD于点F,交DC的延长线于G.
如图,直线AG过平行四边形ABCD的边BC的中点F、交对角线BD于点F,交DC的延长线于G.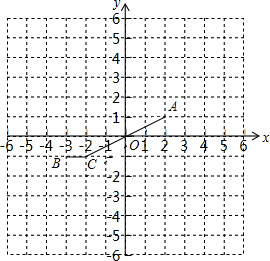 若A、B、C、D四点构成平行四边形A(2,1)、B(-3,1)、C(-2,-1),则顶点D的坐标为(3,1)或(1,1)或(-5,-3).
若A、B、C、D四点构成平行四边形A(2,1)、B(-3,1)、C(-2,-1),则顶点D的坐标为(3,1)或(1,1)或(-5,-3).