题目内容
17.已知关于x的一元二次方程x2-3x+1-k=0有两个不相等的实数根.(1)求k的取值范围;
(2)若k为负整数,求此时方程的根.
分析 (1)要使方程有两个不相等的实数根,只需根的判别式大于0即可;
(2)由k为负整数可得到k的值,代入原方程,然后解这个方程即可.
解答 解:(1)由题可得:(-3)2-4(1-k)>0,
解得k>-$\frac{5}{4}$;
(2)若k为负整数,则k=-1,
此时原方程为x2-3x+2=0,
解得x1=1,x2=2.
点评 本题主要考查了根的判别式,解一元一次不等式、解一元二次方程等知识,对于一元二次方程ax2+bx+c=0(a≠0),则有b2-4ac≥0?方程有两实根,b2-4ac>0?方程有两不等实根,b2-4ac=0?方程有两相等实根,b2-4ac<0?方程没有实根.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
8.2的平方根是( )
| A. | ±$\sqrt{2}$ | B. | $\sqrt{2}$ | C. | ±1.414 | D. | 4 |
12.某校师生植树节积极参加以组为单位的植树活动,七个小组植树情况如下:
则本组数据的众数与中位数分别为( )
| 第一组 | 第二组 | 第三组 | 第四组 | 第五组 | 第六组 | 第七组 | |
| 数量(棵) | 5 | 6 | 5 | 4 | 6 | 5 | 7 |
| A. | 5,4 | B. | 6,5 | C. | 7,6 | D. | 5,5 |




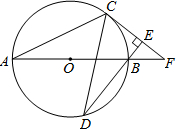 如图,AB为⊙O的直径,C,D为⊙O上不同于A,B的两点,过点C作⊙O的切线CF交直线AB于点F,直线DB⊥CF于点E.
如图,AB为⊙O的直径,C,D为⊙O上不同于A,B的两点,过点C作⊙O的切线CF交直线AB于点F,直线DB⊥CF于点E.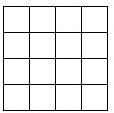 如图,将3枚相同硬币依次放入一个4×4的正方形格子中(每个正方形格子只能放1枚硬币).求所放的3枚硬币中,任意两个都不同行且不同列的概率.
如图,将3枚相同硬币依次放入一个4×4的正方形格子中(每个正方形格子只能放1枚硬币).求所放的3枚硬币中,任意两个都不同行且不同列的概率. 如图,己知△ABC是等腰直角三角形,AC=BC,∠ACB=90°,AE⊥EF于E,BF⊥EF于F,求证:EF=AE+BF.
如图,己知△ABC是等腰直角三角形,AC=BC,∠ACB=90°,AE⊥EF于E,BF⊥EF于F,求证:EF=AE+BF.