题目内容
19. 如图,已知△ABC的三个内角的平分线交于点O,点D在CA的延长线上,且DC=BC,若∠BAC=80°,则∠BOD的度数为100°.
如图,已知△ABC的三个内角的平分线交于点O,点D在CA的延长线上,且DC=BC,若∠BAC=80°,则∠BOD的度数为100°.
分析 如图在CO的延长线上取一点H.首先证明∠DOB=∠D+∠OBC+∠OCD+∠OCB=∠D+∠OBC+∠ACB,由△OCD≌△OCB,推出∠D=∠OBC=∠ABO,推出∠DOB=∠ABC+∠ACB=180°-∠BAC,延长即可解决问题.
解答 解:如图在CO的延长线上取一点H.
∵∠DOH=∠D+∠DCO,∠BOH=∠OBC+∠OCB,
∴∠DOB=∠D+∠OBC+∠OCD+∠OCB=∠D+∠OBC+∠ACB,
∵O是内心,
∴∠DCO=∠BCO,
在△OCD和△OCB中,
$\left\{\begin{array}{l}{OC=OC}\\{∠OCD=∠OCB}\\{CD=CB}\end{array}\right.$,
∴△OCD≌△OCB,
∴∠D=∠OBC=∠ABO,
∴∠DOB=∠ABC+∠ACB=180°-∠BAC=100°,
故答案为100°.
点评 本题考查全等三角形的判定和性质、三角形的内心的性质,三角形的外角的性质等知识,解题的关键是证明∠DOB=∠ABC+∠ACB=180°-∠BAC.属于中考常考题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.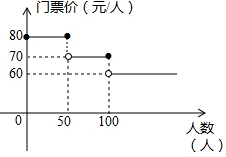 某中学七年级组织学生进行春游,景点门票价格情况如图,则下列说法正确的是( )
某中学七年级组织学生进行春游,景点门票价格情况如图,则下列说法正确的是( )
 某中学七年级组织学生进行春游,景点门票价格情况如图,则下列说法正确的是( )
某中学七年级组织学生进行春游,景点门票价格情况如图,则下列说法正确的是( )| A. | 当旅游人数为50时,则门票价格为70元/人 | |
| B. | 当旅游人数为50或者100的时,门票价格都是70元/人 | |
| C. | 两个班级都是40名学生,则两个班联合起来购票比分别购票要便宜 | |
| D. | 当人数增多时,虽然门票价格越来越低,但是购票总费用会越来越高 |
7.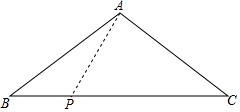 如图,等腰三角形ABC的底边长为8cm,腰长为5cm,一动点P在底边上从点B向点C以1cm/s的速度移动,
如图,等腰三角形ABC的底边长为8cm,腰长为5cm,一动点P在底边上从点B向点C以1cm/s的速度移动,
(1)求△ABC的面积;
(2)请你探究:当点P运动几秒时,点P与顶点A的连线PA与腰垂直?
 如图,等腰三角形ABC的底边长为8cm,腰长为5cm,一动点P在底边上从点B向点C以1cm/s的速度移动,
如图,等腰三角形ABC的底边长为8cm,腰长为5cm,一动点P在底边上从点B向点C以1cm/s的速度移动,(1)求△ABC的面积;
(2)请你探究:当点P运动几秒时,点P与顶点A的连线PA与腰垂直?
4.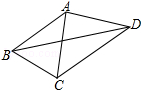 如图,已知AB=AC=AD,∠CBD=2∠BDC,∠BAC=42°,则∠CAD的度数为( )度.
如图,已知AB=AC=AD,∠CBD=2∠BDC,∠BAC=42°,则∠CAD的度数为( )度.
 如图,已知AB=AC=AD,∠CBD=2∠BDC,∠BAC=42°,则∠CAD的度数为( )度.
如图,已知AB=AC=AD,∠CBD=2∠BDC,∠BAC=42°,则∠CAD的度数为( )度.| A. | 56 | B. | 78 | C. | 84 | D. | 112 |
 如图,将一个多边形按图所示减掉一个角,所得多边形的内角和为1800°,求原多边形的边数.
如图,将一个多边形按图所示减掉一个角,所得多边形的内角和为1800°,求原多边形的边数. 如图,AB为⊙O的弦,AB=6,点C是⊙O上的一个动点,且△ACB=45°,若点M、N分别是AB、BC的中点,求MN长的最大值.
如图,AB为⊙O的弦,AB=6,点C是⊙O上的一个动点,且△ACB=45°,若点M、N分别是AB、BC的中点,求MN长的最大值.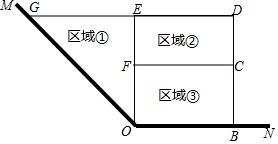 为了节省材料,某水产养殖户利用水库的一角∠MON(∠MON=135°)的两边为边,用总长为120m的围网在水库中围成了如图所示的①②③三块区域,其中区域①为直角三角形,区域②③为矩形,而且四边形OBDG为直角梯形.
为了节省材料,某水产养殖户利用水库的一角∠MON(∠MON=135°)的两边为边,用总长为120m的围网在水库中围成了如图所示的①②③三块区域,其中区域①为直角三角形,区域②③为矩形,而且四边形OBDG为直角梯形. 如图,∠1=∠B,∠2=138°,则∠EDF=42°.
如图,∠1=∠B,∠2=138°,则∠EDF=42°.