题目内容
7.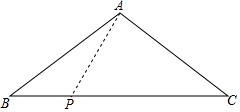 如图,等腰三角形ABC的底边长为8cm,腰长为5cm,一动点P在底边上从点B向点C以1cm/s的速度移动,
如图,等腰三角形ABC的底边长为8cm,腰长为5cm,一动点P在底边上从点B向点C以1cm/s的速度移动,(1)求△ABC的面积;
(2)请你探究:当点P运动几秒时,点P与顶点A的连线PA与腰垂直?
分析 (1)根据等腰三角形三线合一性质可得到BD的长,由勾股定理可求得AD的长,根据三角形面积公式即可求解;
(2)分两种情况进行分析:①PA⊥AC②PA⊥AB,从而可得到运动的时间.
解答 解:(1)作AD⊥BC
∵AB=AC=5,BC=8,
∴BD=$\frac{1}{2}$BC=4,
∴AD=$\sqrt{A{B^2}-B{D^2}}=\sqrt{{5^2}-{4^2}_{\;}}=3$,
∴${S_{△ABC}}=\frac{1}{2}BC•AD=12(c{m^2})$;
(2)分两种情况: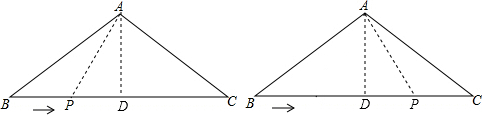
当点P运动t秒后有PA⊥AC时,
∵AP2=PD2+AD2=PC2-AC2,
∴PD2+AD2=PC2-AC2,
∴PD2+32=(PD+42-52,
∴PD=2.25,
∴BP=4-2.25=1.75=1t,
∴t=1.75,
当点P运动t秒后有PA⊥AB时,同理可证得PD=2.25,
∴BP=4+2.25=6.25,
∴t=6.25.
综上所述,当P运动1.75s或6.25s秒时,P点与顶点A的连线PA与腰垂直.
点评 此题考查了等腰三角形的性质和勾股定理的运用,此题难度适中,解题的关键是分类讨论思想、方程思想与数形结合思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.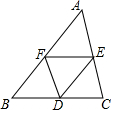 如图,D、E、F是△ABC三边的中点,且DE∥AB,DF∥AC,EF∥BC,平移△AEF可以得到的三角形是( )
如图,D、E、F是△ABC三边的中点,且DE∥AB,DF∥AC,EF∥BC,平移△AEF可以得到的三角形是( )
 如图,D、E、F是△ABC三边的中点,且DE∥AB,DF∥AC,EF∥BC,平移△AEF可以得到的三角形是( )
如图,D、E、F是△ABC三边的中点,且DE∥AB,DF∥AC,EF∥BC,平移△AEF可以得到的三角形是( )| A. | △BDF | B. | △DEF | C. | △CDE | D. | △BDF和△CDE |
 如图是一个育苗棚,棚宽a=12m,棚高b=5m,棚长d=10m,则覆盖在棚斜面上的塑料薄膜的面积为130m2.
如图是一个育苗棚,棚宽a=12m,棚高b=5m,棚长d=10m,则覆盖在棚斜面上的塑料薄膜的面积为130m2. 如图,在等腰△ABC中,AB=AC,点D,E分别是BC,AB边的中点,过A点作AF∥BC交DE的延长线于F点,连接AD,BF.
如图,在等腰△ABC中,AB=AC,点D,E分别是BC,AB边的中点,过A点作AF∥BC交DE的延长线于F点,连接AD,BF.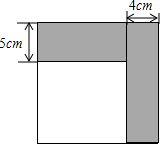 如图所示,小明将一张正方形纸片剪去一条宽为4cm的长条后,再从剩下的长方形纸片上剪去一条宽为5cm的长条.如果两次剪下的长条面积正好相等.
如图所示,小明将一张正方形纸片剪去一条宽为4cm的长条后,再从剩下的长方形纸片上剪去一条宽为5cm的长条.如果两次剪下的长条面积正好相等. 如图,已知△ABC的三个内角的平分线交于点O,点D在CA的延长线上,且DC=BC,若∠BAC=80°,则∠BOD的度数为100°.
如图,已知△ABC的三个内角的平分线交于点O,点D在CA的延长线上,且DC=BC,若∠BAC=80°,则∠BOD的度数为100°.