题目内容

4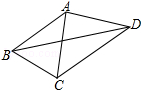．如图，已知AB=AC=AD，∠CBD=2∠BDC，∠BAC=42°，则∠CAD的度数为（　　）度．
A．56B．78C．84D．112

分析 首先以A为圆心，AB长为半径画弧，然后可确定B、C、D同在⊙A上，再根据∠CBD=2∠BDC可得$\widehat{CD}$=2$\widehat{BC}$，然后可得∠CAD=2∠BAC=84°．

解答 解：以A为圆心，AB长为半径画弧，
∵AB=AC=AD，
∴B、C、D同在⊙A上，
∵∠CBD=2∠BDC，
∴$\widehat{CD}$=2$\widehat{BC}$，
∴∠CAD=2∠BAC=84°，
故选：C．

点评 此题主要考查了圆周角定理，关键是掌握在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．

练习册系列答案
相关题目
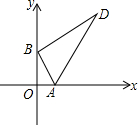14．Rt△ABD的两顶点A、B分别在x轴和y轴上运动，其中∠ABD=90°，∠D=30°，AB=4，则顶点D到原点O的距离的最小值为2$\sqrt{13}$-2，顶点D到原点O的距离的最大值为2$\sqrt{13}$+2．
15．如图是一个育苗棚，棚宽a=12m，棚高b=5m，棚长d=10m，则覆盖在棚斜面上的塑料薄膜的面积为130m2．
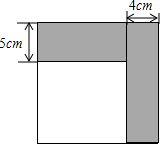12．如图所示，小明将一张正方形纸片剪去一条宽为4cm的长条后，再从剩下的长方形纸片上剪去一条宽为5cm的长条．如果两次剪下的长条面积正好相等．
（1）设这个正方形的边长为xcm，则宽为4cm的长条的长为xcm，宽为5cm的长条的长为x-4cm，根据题意可列方程为4x=5（x-4）；
（2）求每一条长条的面积．
19．如图，已知△ABC的三个内角的平分线交于点O，点D在CA的延长线上，且DC=BC，若∠BAC=80°，则∠BOD的度数为100°．
9．长为1，宽为a的矩形纸片（0＜a＜$\frac{1}{2}$），如图那样折一下，剪下一个边长等于矩形宽度的正方形（称为第一次操作）；再把剩下的矩形如图那样折一下，剪下一个边长等于此时矩形宽度的正方形（称为第二次操作）；如此反复操作下去．若在第n次操作后，剩下的矩形为正方形，则操作终止．当n=3时，a的值为$\frac{3}{5}$或$\frac{3}{4}$．
16．某镇正在建造的文化广场工地上，有两种铺设广场地面的材料：一种是长为a cm，宽为b cm的长方形板材（如图1），另一种是边长为C cm的正方形地砖（图2）．

（1）用多少块如图2所示的正方形地砖能拼出一个新的正方形？（只要写出一个符合条件的答案即可），并写出新正方形的面积；
（2）用如图1所示的四块长方形板材铺成如图3的大长方形或如图4的大正方形，中间分别空出一个小长方形和小正方形（即图中阴影部分）；
①试比较中间的小长方形和中间的小正方形的面积哪个大？大多少？
②如图4，已知大正方形的边长比中间的小正方形的边长多20cm，面积大3200cm2．如果选用如图2所示的正方形地砖（边长为20cm）铺设图4中间的小正方形部分，那么能否做到不用切割地砖就可直接密铺（缝隙忽略不计）呢？若能，请求出密铺所需地砖的块数；若不能，至少要切割几块如图2的地砖？
13．下列各个图中，一定全等的是（　　）
A．各有一个角是45°的两个等腰三角形
B．两个等边三角形
C．各有一个角是45°，腰长都是3cm的两个等腰三角形
D．腰和顶角对应相等的两个等腰三角形
14．下列各组两项中，是同类项的是（　　）
A．-2xy与-3abB．$\frac{1}{5}$abc与$\frac{1}{5}$acC．xy与-xyD．3x2y与3xy2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网