题目内容
7.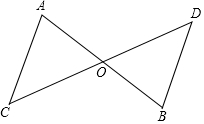 如图,AB与CD相交于点O,AC∥BD,AO=OB,求证:CO=OD.
如图,AB与CD相交于点O,AC∥BD,AO=OB,求证:CO=OD.
分析 根据已知利用AAS判定△AOC≌△BOD,再根据全等三角形的对应边相等即可得到OC=OD.
解答 证明:∵AC∥BD,
∴∠A=∠B.
在△AOC与△BOD中,$\left\{\begin{array}{l}{∠A=∠B}\\{OA=OB}\\{∠AOC=∠BOD}\end{array}\right.$
∴△AOC≌△BOD(ASA).
∴OC=OD.
点评 本题考查全等三角形的判定及性质的运用,内错角相等两直线平行的判定方法的运用,解答时证明三角形全等是关键.

练习册系列答案
相关题目
18. 如图,AB、AC是⊙O的两条弦,∠A=30°,过点C的切线与OB的延长线交于点D,则∠D的度数为( )
如图,AB、AC是⊙O的两条弦,∠A=30°,过点C的切线与OB的延长线交于点D,则∠D的度数为( )
 如图,AB、AC是⊙O的两条弦,∠A=30°,过点C的切线与OB的延长线交于点D,则∠D的度数为( )
如图,AB、AC是⊙O的两条弦,∠A=30°,过点C的切线与OB的延长线交于点D,则∠D的度数为( )| A. | 30° | B. | 35° | C. | 40° | D. | 45° |
19.某商场销售一批衬衫,平均每天可售出20件,每件盈利40元.为了扩大销售,增加盈利,商场采取了降价措施,假设在一定范围内,衬衫的单价每降1元,商场平均每天可多售出2件.如果降价后商场销售这批衬衫每天盈利1 250元,衬衫的单价降了x元,那么下面所列的方程正确的是( )
| A. | (20+x)(40-2x)=1250 | B. | (20+x)(40-x)=1250 | C. | (20+2x)(40-2x)=1250 | D. | (20+2x)(40-x)=1250 |
16.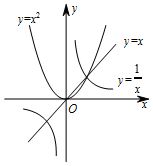 给出下列命题及函数y=x,y=x2和y=$\frac{1}{x}$的图象
给出下列命题及函数y=x,y=x2和y=$\frac{1}{x}$的图象
①如果$\frac{1}{a}$>a>a2,那么0<a<1;
②如果a2>a>$\frac{1}{a}$,那么a>1;
③如果$\frac{1}{a}$>a2>a,那么-1<a<0;
④如果a2>$\frac{1}{a}$>a时,那么a<-1.
则( )
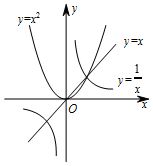 给出下列命题及函数y=x,y=x2和y=$\frac{1}{x}$的图象
给出下列命题及函数y=x,y=x2和y=$\frac{1}{x}$的图象①如果$\frac{1}{a}$>a>a2,那么0<a<1;
②如果a2>a>$\frac{1}{a}$,那么a>1;
③如果$\frac{1}{a}$>a2>a,那么-1<a<0;
④如果a2>$\frac{1}{a}$>a时,那么a<-1.
则( )
| A. | 正确的命题是①④ | B. | 错误的命题是②③④ | C. | 正确的命题是①② | D. | 错误的命题只有③ |
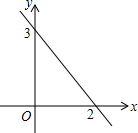 一次函数y=kx+b(k≠0)的图象如图所示,当x=0时,y的值是3.
一次函数y=kx+b(k≠0)的图象如图所示,当x=0时,y的值是3.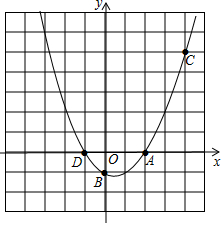 如图,已知二次函数y=ax2+bx+c经过点A(2,0),B(0,-1),C(4,5)三点.
如图,已知二次函数y=ax2+bx+c经过点A(2,0),B(0,-1),C(4,5)三点.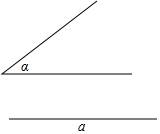 如图,已知∠α和线段a,求作△ABC,使BC=a,∠B=∠C=$\frac{1}{2}$α(只保留作图痕迹,不要求写出作法)
如图,已知∠α和线段a,求作△ABC,使BC=a,∠B=∠C=$\frac{1}{2}$α(只保留作图痕迹,不要求写出作法)