题目内容
14.若抛物线y=x2+2(k-1)x+3,当x<0时,y随x的增大而减小,求k的取值范围.分析 根据二次函数的系数大于零,在对称轴的左侧,y随x的增大而减小,可得答案.
解答 解:由抛物线y=x2+2(k-1)x+3.当x<0时,y随x的增大而减小,得
-$\frac{2(k-1)}{2}$≥0,
解得k≤1.
故k的取值范围为k≤1.
点评 本题考查了二次函数的性质,二次函数y=ax2+bx+c(a,b,c为常数,a≠0),当a>0时,在对称轴左侧y随x的增大而减小,在对称轴右侧y随x的增大而增大;当a<0时,在对称轴左侧y随x的增大而增大,在对称轴右侧y随x的增大而减小.正比例函数中当k>0时,y随x的增大而增大,k<0时,y随x的怎大而减小.

练习册系列答案
相关题目
9.在-1,0,2,$\sqrt{3}$四个数中,最大的数是( )
| A. | -1 | B. | 0 | C. | 2 | D. | $\sqrt{3}$ |
4.将抛物线y=-x2向左平移1个单位,再向下平移2个单位,所得抛物线的函数关系式是( )
| A. | y=-(x-1)2-2 | B. | y=-(x-1)2+2 | C. | y=-(x+1)2-2 | D. | y=-(x+1)2-2 |
 如图是由四个大小相同的立方体组成的几何体,则这个几何体的左视图是( )
如图是由四个大小相同的立方体组成的几何体,则这个几何体的左视图是( )




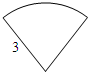 如图,半径为3cm的扇形纸片的周长为10cm,将它围成一个圆锥的侧面,则圆锥的底面圆的半径等于$\frac{2}{π}$cm.(结果保留π)
如图,半径为3cm的扇形纸片的周长为10cm,将它围成一个圆锥的侧面,则圆锥的底面圆的半径等于$\frac{2}{π}$cm.(结果保留π)