Question

8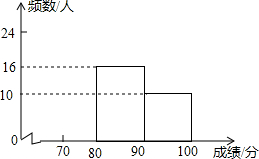．为了让读书成为习惯，某中学开展了读书征文比赛．经过评选，共有50篇征文获奖．现将评奖情况统计如下：

等级	成绩（用S表示）	频数	频率
一等奖	90≤S≤100	10	a
二等奖	80≤S＜90	16	b
三等奖	70≤S＜80	c	0.48
合计		50	1

请根据以上提供的信息，解答下列问题：
（1）求出统计表中a，b，c的值；
（2）补全频数分布直方图；
（3）若初一年级的两男、两女四名同学获得一等奖，现从四人中随机抽取两人让他们谈谈参赛体会，请用画树状图或列表的方法求出恰好抽到两名男生的概率．

Answer 1

分析 （1）观察表格，根据频率的定义求解即可求得答案；
（2）结合（1）可得c=24，继而可补全频数分布直方图；
（3）首先根据题意画出树状图，然后由树状图求得所有等可能的结果与恰好抽到两名男生的情况，再利用概率公式即可求得答案．

解答 解：（1）a=10÷50=0.2，
b=16÷50=0.32，
c=50×0.48=24；

（2）如图：


（3）画树状图得：

∵共有12种等可能的结果，恰好抽到两名男生的有2种情况，
∴恰好抽到两名男生的概率为：$\frac{2}{12}$=$\frac{1}{6}$．

点评 此题考查了树状图法与列表法求概率以及频率分布直方图．用到的知识点为：概率=所求情况数与总情况数之比．