题目内容
20.已知2a-b+7的平方根是±5,2a+b-1的算术平方根是4,求-a+b的值.分析 根据平方根的平等于被开方数,可得二元一次方程,根据加减法,可得答案.
解答 解:依题意知:
2a-b+7=25,即2a-b=18 ①
2a+b-1=16,即2a+b=17 ②
由②+①得 4a=35,
解得:a=8.75,
把a=8.75代入②得:b=-0.5,
把a=8.75,b=-0.5代入-a+b=-8.75-0.5=-9.25.
点评 本题考查了平方根,利用平方根的平方等于被开方数得出方程是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.下列说法中,不正确的是( )
| A. | 10的立方根是$\root{3}{10}$ | B. | -2是4的一个平方根 | ||
| C. | $\frac{4}{9}$的平方根是$\frac{2}{3}$ | D. | 0.01的算术平方根是0.1 |
8.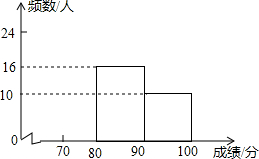 为了让读书成为习惯,某中学开展了读书征文比赛.经过评选,共有50篇征文获奖.现将评奖情况统计如下:
为了让读书成为习惯,某中学开展了读书征文比赛.经过评选,共有50篇征文获奖.现将评奖情况统计如下:
请根据以上提供的信息,解答下列问题:
(1)求出统计表中a,b,c的值;
(2)补全频数分布直方图;
(3)若初一年级的两男、两女四名同学获得一等奖,现从四人中随机抽取两人让他们谈谈参赛体会,请用画树状图或列表的方法求出恰好抽到两名男生的概率.
 为了让读书成为习惯,某中学开展了读书征文比赛.经过评选,共有50篇征文获奖.现将评奖情况统计如下:
为了让读书成为习惯,某中学开展了读书征文比赛.经过评选,共有50篇征文获奖.现将评奖情况统计如下:| 等级 | 成绩(用S表示) | 频数 | 频率 |
| 一等奖 | 90≤S≤100 | 10 | a |
| 二等奖 | 80≤S<90 | 16 | b |
| 三等奖 | 70≤S<80 | c | 0.48 |
| 合计 | 50 | 1 |
(1)求出统计表中a,b,c的值;
(2)补全频数分布直方图;
(3)若初一年级的两男、两女四名同学获得一等奖,现从四人中随机抽取两人让他们谈谈参赛体会,请用画树状图或列表的方法求出恰好抽到两名男生的概率.
5.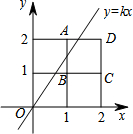 将2×2的正方形网格如图放置在平面直角坐标系中,每个小正方形的顶点称为格点,每个小正方形的边长都是1,正方形ABCD的顶点都在格点上.若直线y=kx(k≠0)与正方形ABCD有公共点,则k的取值范围是( )
将2×2的正方形网格如图放置在平面直角坐标系中,每个小正方形的顶点称为格点,每个小正方形的边长都是1,正方形ABCD的顶点都在格点上.若直线y=kx(k≠0)与正方形ABCD有公共点,则k的取值范围是( )
 将2×2的正方形网格如图放置在平面直角坐标系中,每个小正方形的顶点称为格点,每个小正方形的边长都是1,正方形ABCD的顶点都在格点上.若直线y=kx(k≠0)与正方形ABCD有公共点,则k的取值范围是( )
将2×2的正方形网格如图放置在平面直角坐标系中,每个小正方形的顶点称为格点,每个小正方形的边长都是1,正方形ABCD的顶点都在格点上.若直线y=kx(k≠0)与正方形ABCD有公共点,则k的取值范围是( )| A. | k≤2 | B. | $k≥\frac{1}{2}$ | C. | $\frac{1}{2}≤k≤2$ | D. | $\frac{1}{2}<k<2$ |
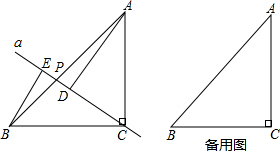
 (1)如图,在△ABC中,AD⊥BC,∠1=∠B,求证:△ABC是直角三角形.
(1)如图,在△ABC中,AD⊥BC,∠1=∠B,求证:△ABC是直角三角形. 如图,在?ABCD中,点E,F在对角线BD上,且四边形AFCE也是平行四边形,你能想办法推理出线段BE与DF相等吗?你有几种方法?并比较一下哪一种方法比较好.
如图,在?ABCD中,点E,F在对角线BD上,且四边形AFCE也是平行四边形,你能想办法推理出线段BE与DF相等吗?你有几种方法?并比较一下哪一种方法比较好.