题目内容
13.已知菱形ABCD一个内角等于120°,BD=2cm,则菱形的边长为2或$\frac{2\sqrt{3}}{3}$cm,面积为2$\sqrt{3}$或$\frac{2\sqrt{3}}{3}$cm2.分析 分两种情况:①当BD为短对角线时,先证明△ABD是等边三角形,得出AB=BD,再由勾股定理求出AC,菱形面积=$\frac{1}{2}$AC•BD,即可求出面积;
②当BD为长对角线时,先由锐角三角函数求出OA,AC,再根据含30°的直角三角形的性质得出AB,根据菱形面积=$\frac{1}{2}$AC•BD,即可得出结果.
解答 解:分两种情况:①当BD为短对角线时,如图1所示: ∵四边形ABCD是菱形,∠ABC=120°,
∵四边形ABCD是菱形,∠ABC=120°,
∴AB=AD,∠BAD=60°,AC⊥BD,OA=$\frac{1}{2}$AC,OB=$\frac{1}{2}$BD=1,
∴△ABD是等边三角形,
∴AB=BD=2cm,
∴OA=$\sqrt{{2}^{2}-{1}^{2}}$=$\sqrt{3}$,
∴AC=2$\sqrt{3}$,
∴菱形ABCD的面积=$\frac{1}{2}$AC•BD=$\frac{1}{2}$×2$\sqrt{3}$×2=2$\sqrt{3}$;
②当BD为长对角线时,如图2所示:
∵四边形ABCD是菱形,∠BCD=120°,
∴AB=AD,∠ABC=60°,AC⊥BD,OA=$\frac{1}{2}$AC,OB=$\frac{1}{2}$BD=1,∠OBA=30°,
∴OA=OB•tan30°=$\frac{\sqrt{3}}{3}$,
∴AB=2OA=$\frac{2\sqrt{3}}{3}$,AC=$\frac{2\sqrt{3}}{3}$,
∴菱形ABCD的面积=$\frac{1}{2}$AC•BD=$\frac{1}{2}$×$\frac{2\sqrt{3}}{3}$×2=$\frac{2\sqrt{3}}{3}$;
故答案为2或$\frac{2\sqrt{3}}{3}$cm;2$\sqrt{3}$或$\frac{2\sqrt{3}}{3}$cm2.
点评 本题考查了菱形的性质、勾股定理的运用、锐角三角函数以及含30°的直角三角形的性质;本题需要分类讨论,避免漏解.

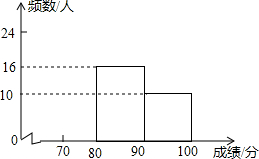 为了让读书成为习惯,某中学开展了读书征文比赛.经过评选,共有50篇征文获奖.现将评奖情况统计如下:
为了让读书成为习惯,某中学开展了读书征文比赛.经过评选,共有50篇征文获奖.现将评奖情况统计如下:| 等级 | 成绩(用S表示) | 频数 | 频率 |
| 一等奖 | 90≤S≤100 | 10 | a |
| 二等奖 | 80≤S<90 | 16 | b |
| 三等奖 | 70≤S<80 | c | 0.48 |
| 合计 | 50 | 1 |
(1)求出统计表中a,b,c的值;
(2)补全频数分布直方图;
(3)若初一年级的两男、两女四名同学获得一等奖,现从四人中随机抽取两人让他们谈谈参赛体会,请用画树状图或列表的方法求出恰好抽到两名男生的概率.
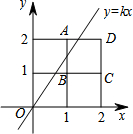 将2×2的正方形网格如图放置在平面直角坐标系中,每个小正方形的顶点称为格点,每个小正方形的边长都是1,正方形ABCD的顶点都在格点上.若直线y=kx(k≠0)与正方形ABCD有公共点,则k的取值范围是( )
将2×2的正方形网格如图放置在平面直角坐标系中,每个小正方形的顶点称为格点,每个小正方形的边长都是1,正方形ABCD的顶点都在格点上.若直线y=kx(k≠0)与正方形ABCD有公共点,则k的取值范围是( )| A. | k≤2 | B. | $k≥\frac{1}{2}$ | C. | $\frac{1}{2}≤k≤2$ | D. | $\frac{1}{2}<k<2$ |
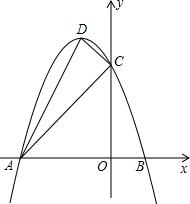 如图,二次函数y=ax2+bx+c(a<0)图象的顶点为D,与x轴的两个交点分别为A、B(A在B左侧),与y轴交于点C(0,3),且OA=3OB,∠ACD=90°
如图,二次函数y=ax2+bx+c(a<0)图象的顶点为D,与x轴的两个交点分别为A、B(A在B左侧),与y轴交于点C(0,3),且OA=3OB,∠ACD=90°