题目内容
18．已知m2+2m-1=0，则代表是m3+$\frac{5}{2}$m2+2014的值为2014$\frac{1}{2}$．分析 已知m2+2m-1=0，得出m2+2m=1，整体代入m3+$\frac{5}{2}$m2+2014求得数值即可．
解答 解：∵m2+2m-1=0，
∴m2+2m=1，
∴m3+$\frac{5}{2}$m2+2014
=m（m2+2m）+$\frac{1}{2}$m2+2014
=$\frac{1}{2}$（m2+2m）+2014
=$\frac{1}{2}$+2014
=2014$\frac{1}{2}$．
故答案为：2014$\frac{1}{2}$．
点评 此题考查因式分解的实际运用，逐步分解是解决问题的关键，注意整体代入思想的渗透．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
8．
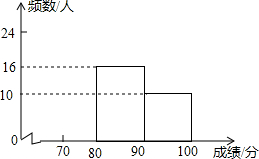为了让读书成为习惯，某中学开展了读书征文比赛．经过评选，共有50篇征文获奖．现将评奖情况统计如下：
请根据以上提供的信息，解答下列问题：
（1）求出统计表中a，b，c的值；
（2）补全频数分布直方图；
（3）若初一年级的两男、两女四名同学获得一等奖，现从四人中随机抽取两人让他们谈谈参赛体会，请用画树状图或列表的方法求出恰好抽到两名男生的概率．
为了让读书成为习惯，某中学开展了读书征文比赛．经过评选，共有50篇征文获奖．现将评奖情况统计如下：| 等级 | 成绩（用S表示） | 频数 | 频率 |
| 一等奖 | 90≤S≤100 | 10 | a |
| 二等奖 | 80≤S＜90 | 16 | b |
| 三等奖 | 70≤S＜80 | c | 0.48 |
| 合计 | 50 | 1 |
（1）求出统计表中a，b，c的值；
（2）补全频数分布直方图；
（3）若初一年级的两男、两女四名同学获得一等奖，现从四人中随机抽取两人让他们谈谈参赛体会，请用画树状图或列表的方法求出恰好抽到两名男生的概率．
如图，在?ABCD中，点E，F在对角线BD上，且四边形AFCE也是平行四边形，你能想办法推理出线段BE与DF相等吗？你有几种方法？并比较一下哪一种方法比较好．
19．若分式$\frac{x+1}{x-2}$的值为0，则x的值为（ ）
| A． | -1 | B． | 0 | C． | 2 | D． | -1或2 |