题目内容
15. 如图,梯形ABCD中,∠ABC和∠DCB的平分线相交于梯形中位线EF上的一点P,PH⊥AB于H.若EF=3,PH=1,AD=2,则△BPC的面积为2.
如图,梯形ABCD中,∠ABC和∠DCB的平分线相交于梯形中位线EF上的一点P,PH⊥AB于H.若EF=3,PH=1,AD=2,则△BPC的面积为2.
分析 如图,作辅助线;首先运用角平分线的性质证明PQ=PH=1;其次运用梯形的中位线定理求出BC的长度,运用三角形的面积公式,即可解决问题.
解答  解:如图,过点P作PQ⊥BC于点Q;
解:如图,过点P作PQ⊥BC于点Q;
∵BP平分∠ABC,且PH⊥AB于点H,
∴PQ=PH=1;设BC=λ,由题意得:
$\frac{2+λ}{2}=3$,解得:λ=4;
∴${S}_{△BPC}=\frac{1}{2}×4×1$=2,
故答案为2.
点评 该题主要考查了梯形的中位线定理、角平分线的性质等几何知识点及其应用问题;解题的方法是作辅助线,将分散的条件集中;解题的关键是灵活运用梯形的中位线定理来解题.

练习册系列答案
相关题目


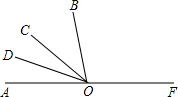 如图,已知O为直线AF上一点,射线OC平分∠AOB,∠COD=20°;
如图,已知O为直线AF上一点,射线OC平分∠AOB,∠COD=20°;