题目内容
20.如图(1),抛物线y=ax2+bx+5(a≠0)与x轴交于A、B两点,与y轴交于点C,直线AC的解析式为y=x+5,抛物线的对称轴与x轴交于点E,点D(-2,-3)在对称轴上.(1)求此抛物线的解析式;
(2)如图(1),若点M是线段OE上一点(点M不与点O、E重合),过点M作MN⊥x轴,交抛物线于点N,记点N关于抛物线对称轴的对称点为点F,点P是线段MN上一点,且满足MN=4MP,连接FN、FP,作QP⊥PF交x轴于点Q,且满足PF=PQ,求点Q的坐标;
(3)如图(2),过点B作BK⊥x轴交直线AC于点K,连接DK、AD,点H是DK的中点,点G是线段AK上任意一点,将△DGH沿GH边翻折得△D′GH,求当KG为何值时,△D′GH与△KGH重叠部分的面积是△DGK面积的$\frac{1}{4}$?

分析 (1)因为点A在y=x+5上,令y=0得出点A坐标,再用待定系数法求二次函数的解析式即可;
(2)可证明△QMP≌△PNF,得出MQ=NP,MP=NF,设M(m,0),得出N(m,-m2-4m+5),利用线段的长度列出方程,求得m的值,根据m的取值范围,得出m=-1,从而求得点Q的坐标;
(3)令y=0,得出点B和K的坐标,分三种情况:①若翻折后,点D′在直线GK上方,记D′H与GK交于点L,连接D'K,由面积的关系得出四边形D'GHK是平行四边形,再证明△ABK和△AED都是等腰直角三角形,由勾股定理得AG和KG即可;②若翻折后,点D′在直线DK下方,记D′G与KH交于点L,连接D′K,由题意得S△GHL=$\frac{1}{4}$S△DGK=$\frac{1}{2}$S△GHK=$\frac{1}{2}$S△GHD′,即S△GHL=S△D′HL=S△KGL,仍证明四边形D′KGH是平行四边形,求得KG;③若翻折后,点D′于点K重合,则重叠部分的面积等于S△KGH=$\frac{1}{2}$S△DGK,不合题意;综合写出KG的值.
解答 解:(1)在y=x+5中,令y=0,得x=-5,
∴A(-5,0),
∵D(-2,-3)在对称轴上,
∴抛物线的对称轴为直线x=-2,
∴$\left\{\begin{array}{l}{25a-5b+5=0}\\{-\frac{b}{2a}=-2}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-1}\\{b=-4}\end{array}\right.$,
∴抛物线的解析式为y=-x2-4x+5;
(2)∵MN⊥QM,MN⊥FN,QP⊥PF,如图1,
∴∠2=∠6=90°,∠1+∠3=90°,∠3+∠5=90°,
∴∠1=∠5
又∵PF=PQ,
∴△QMP≌△PNF,
∴MQ=NP,MP=NF,
设M(m,0)(-2<m<0),则N(m,-m2-4m+5),MN=-m2-4m+5
∴F(-4-m,-m2-4m+5),FN=m-(-4-m)=2m+4,
∴-m2-4m+5=4(2m+4),
解得m=-1或m=-11(舍),
∴MN=8,M(-1,0),
∴MQ=NP=$\frac{3}{4}$MN=6,
∴Q(-7,0);
(3)令-x2-4x+5=0,得x=-5或x=1,
∴B(1,0),K(1,6),
∵$DK=\sqrt{{{[{1-(-2)}]}^2}+{{[{6-(-3)}]}^2}}=3\sqrt{10}$,
①若翻折后,点D′在直线GK上方,记D′H与GK交于点L,连接D'K,如图2,
∴${S_{△GHL}}=\frac{1}{4}{S_{△DGK}}=\frac{1}{2}{S_{△GHK}}=\frac{1}{2}{S_{△GHD'}}$,即S△GHL=S△D'GL=S△KHL,
∴GL=LK,HL=D'L,
∴四边形D'GHK是平行四边形,
∴$DG=D'G=KH=\frac{1}{2}KD=\frac{3}{2}\sqrt{10}$,
又∵BK=BA=6,DE=AE=3,
∴△ABK和△AED都是等腰直角三角形,AD=3$\sqrt{2}$,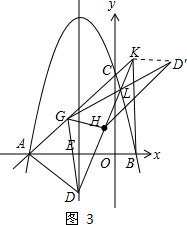
∴∠DAG=45°+45°=90°,
由勾股定理得:$AG=\sqrt{D{G^2}-A{D^2}}=\frac{3}{2}\sqrt{2}$,
∴$KG=KA-AG=6\sqrt{2}-\frac{3}{2}\sqrt{2}=\frac{9}{2}\sqrt{2}$,
②若翻折后,点D′在直线DK下方,记D′G与KH交于点L,连接D′K,如图3,
∴S△GHL=$\frac{1}{4}$S△DGK=$\frac{1}{2}$S△GHK=$\frac{1}{2}$S△GHD′,即S△GHL=S△D′HL=S△KGL,
∴HL=KL,GL=D′L,
∴四边形D′KGH是平行四边形,
∴KG=D′H=DH=$\frac{1}{2}$KD=$\frac{3\sqrt{10}}{2}$,
③若翻折后,点D′于点K重合,则重叠部分的面积等于S△KGH=$\frac{1}{2}$S△DGK,不合题意;
综上所述,KG=$\frac{9}{2}$$\sqrt{2}$或KG=$\frac{3\sqrt{10}}{2}$.
点评 本题综合性的考查了用待定系数法求抛物线的解析式、用公式法求抛物线的顶点坐标、等腰三角形的判定和性质、直角三角形的判定和性质、勾股定理的运用以及全等三角形的判定和性质,题目的综合性很强.难度很大,对学生的解题能力要求较高.

 口算题天天练系列答案
口算题天天练系列答案 一平面镜以与水平面成45°角固定在水平面上,如图所示,一小球以1米/秒的速度沿桌面向平面镜匀速滚去,则小球在平面镜里所成的像将竖直向下.
一平面镜以与水平面成45°角固定在水平面上,如图所示,一小球以1米/秒的速度沿桌面向平面镜匀速滚去,则小球在平面镜里所成的像将竖直向下. 如图,梯形ABCD中,∠ABC和∠DCB的平分线相交于梯形中位线EF上的一点P,PH⊥AB于H.若EF=3,PH=1,AD=2,则△BPC的面积为2.
如图,梯形ABCD中,∠ABC和∠DCB的平分线相交于梯形中位线EF上的一点P,PH⊥AB于H.若EF=3,PH=1,AD=2,则△BPC的面积为2. 写出二次函数y=x2-x-2的图象顶点坐标和对称轴的位置,求出它的最大值或最小值,并画出它的图象.
写出二次函数y=x2-x-2的图象顶点坐标和对称轴的位置,求出它的最大值或最小值,并画出它的图象. 如图,在?ABCD中,已知AB=$\sqrt{3}$,BC=$\sqrt{7}$,∠BAC=90°,求OB的长.
如图,在?ABCD中,已知AB=$\sqrt{3}$,BC=$\sqrt{7}$,∠BAC=90°,求OB的长.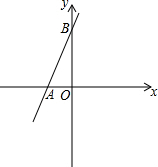 如图,直线y=2x+4与x轴相交于点A,与y轴相交于点B.
如图,直线y=2x+4与x轴相交于点A,与y轴相交于点B.