题目内容
7.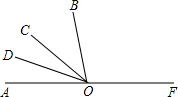 如图,已知O为直线AF上一点,射线OC平分∠AOB,∠COD=20°;
如图,已知O为直线AF上一点,射线OC平分∠AOB,∠COD=20°;(1)若∠AOB=80°,试说明OD为∠AOC的角平分线;
(2)若∠BOD=60°,求∠COF的度数.
分析 (1)因为射线OC平分∠AOB,所以∠AOC=∠BOC=$\frac{1}{2}$∠AOB=40°,根据∠AOD=∠AOC-∠COD=40°-20°=20°,∠COD=20°,所以∠AOD=∠COD,所以OD为∠AOC的角平分线;
(2)先根据∠BOD=60°,∠COD=20°,得到∠BOC=∠BOD-∠COD=60°-20°=40°,因为射线OC平分∠AOB,所以∠AOB=2∠BOC=80°,所以∠BOF=180°-∠AOB=180°-80°=100°,所以∠COF=∠BOF+∠BOC=100°+40°=140°.
解答 解:(1)∵射线OC平分∠AOB,
∴∠AOC=∠BOC=$\frac{1}{2}$∠AOB=40°,
∵∠AOD=∠AOC-∠COD=40°-20°=20°,∠COD=20°,
∴∠AOD=∠COD,
∴OD为∠AOC的角平分线;
(2)∵∠BOD=60°,∠COD=20°,
∴∠BOC=∠BOD-∠COD=60°-20°=40°,
∵射线OC平分∠AOB,
∴∠AOB=2∠BOC=80°,
∴∠BOF=180°-∠AOB=180°-80°=100°,
∴∠COF=∠BOF+∠BOC=100°+40°=140°.
点评 本题考查了角平分线的定义,解决本题的关键是熟记角平分线的定义.

练习册系列答案
 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
19. 下表中的数据是使用了某种调查方法获得的:
下表中的数据是使用了某种调查方法获得的:
初中男生身高情况抽样调查表
(1)根据表中的数据填写表中的空格;
(2)根据填写的数据,在右图中绘制频数分布直方图与频数分布折线图.
 下表中的数据是使用了某种调查方法获得的:
下表中的数据是使用了某种调查方法获得的:初中男生身高情况抽样调查表
| 年级 人数 身高(cm) | 七年级 | 八年级 | 九年级 | 总计(频数) |
| 143-153 | 12 | 3 | 0 | 15 |
| 153-163 | 18 | 9 | 6 | 33 |
| 163-173 | 24 | 33 | 39 | 96 |
| 173-183 | 6 | 15 | 12 | 33 |
| 183-193 | 0 | 0 | 3 | 3 |
| 注:每组可含最低值,不含最高值 | ||||
(2)根据填写的数据,在右图中绘制频数分布直方图与频数分布折线图.
 如图,梯形ABCD中,∠ABC和∠DCB的平分线相交于梯形中位线EF上的一点P,PH⊥AB于H.若EF=3,PH=1,AD=2,则△BPC的面积为2.
如图,梯形ABCD中,∠ABC和∠DCB的平分线相交于梯形中位线EF上的一点P,PH⊥AB于H.若EF=3,PH=1,AD=2,则△BPC的面积为2. 如图,在Rt△ABC中,∠ACB=90°,AC=BC=2,以BC为直径的半圆交AB于D,P是$\widehat{CD}$上的一个动点,连接AP,求AP的最小值.
如图,在Rt△ABC中,∠ACB=90°,AC=BC=2,以BC为直径的半圆交AB于D,P是$\widehat{CD}$上的一个动点,连接AP,求AP的最小值. 写出二次函数y=x2-x-2的图象顶点坐标和对称轴的位置,求出它的最大值或最小值,并画出它的图象.
写出二次函数y=x2-x-2的图象顶点坐标和对称轴的位置,求出它的最大值或最小值,并画出它的图象.