题目内容
3. 完成下面的证明过程
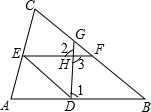
完成下面的证明过程如图,已知∠1+∠2=180°,∠B=∠DEF,求证:DE∥BC.
证明:∵∠1+∠2=180°(已知),
而∠2=∠3(对顶角相等),
∴∠1+∠3=180°
∴EF∥AB(同旁内角互补两直线平行)
∴∠B=∠CFE(两直线平行同位角相等)
∵∠B=∠DEF(已知)
∴∠DEF=∠CFE(等量代换)
∴DE∥BC(内错角相等两直线平行)
分析 先由对顶角相等可得:∠2=∠3,然后由∠1+∠2=180°,根据等量代换可得:∠1+∠3=180°,然后根据同旁内角互补两直线平行可得:EF∥AB,然后根据两直线平行同位角相等可得:∠B=∠CFE,然后由∠B=∠DEF,根据等量代换可得:∠CFE=∠DEF,然后根据内错角相等两直线平行即可得到:DE∥BC.
解答 证明:∵∠1+∠2=180°(已知),
而∠2=∠3(对顶角相等),
∴∠1+∠3=180°
∴EF∥AB(同旁内角互补两直线平行)
∴∠B=∠CFE(两直线平行同位角相等)
∵∠B=∠DEF(已知)
∴∠DEF=∠CFE(等量代换)
∴DE∥BC(内错角相等两直线平行).
故答案为:对顶角相等;EF;AB;同旁内角互补两直线平行;∠CFE;两直线平行同位角相等;∠CFE;内错角相等两直线平行.
点评 此题考查了平行线的性质与判定,熟记同位角相等?两直线平行,内错角相等?两直线平行,同旁内角互补?两直线平行是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.下列四个数中,与$\sqrt{11}$-2的值最接近的数是( )
| A. | $\frac{1}{2}$ | B. | 0 | C. | $\frac{3}{2}$ | D. | 2 |
 如图,在平行四边形ABCD中,DE平分∠ADC,AD=8,BE=4,则平行四边形ABCD的周长是24.
如图,在平行四边形ABCD中,DE平分∠ADC,AD=8,BE=4,则平行四边形ABCD的周长是24.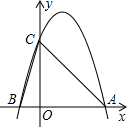 如图所示,二次函数y=-2x2+4x+m的图象与x轴的一个交点为A(3,0),另一个交点为B,且与y轴交于点C.
如图所示,二次函数y=-2x2+4x+m的图象与x轴的一个交点为A(3,0),另一个交点为B,且与y轴交于点C. 如图,正六边形ABCDEF能由△ABO平移得到的图形有哪几个?
如图,正六边形ABCDEF能由△ABO平移得到的图形有哪几个?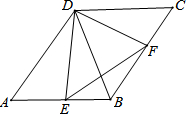 如图,在?ABCD中,∠A=60°,DE⊥AB,DF⊥BC,垂足分别为点E,F,有下列结论:
如图,在?ABCD中,∠A=60°,DE⊥AB,DF⊥BC,垂足分别为点E,F,有下列结论: