题目内容
15.下列四个数中,与$\sqrt{11}$-2的值最接近的数是( )| A. | $\frac{1}{2}$ | B. | 0 | C. | $\frac{3}{2}$ | D. | 2 |
分析 先估算出$\sqrt{11}$是在3与4之间,再减去2应在1与2之间,再根据所给出的选项即可得出答案.
解答 解:∵3<$\sqrt{11}$<4,
∴1<$\sqrt{11}$-2<2,
∴与$\sqrt{11}$-2的值最接近的数是$\frac{3}{2}$.
故选C.
点评 本题主要考查了无理数的估算,解题关键是确定无理数的整数部分即可解决问题.

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
6.下列命题中正确的是( )
| A. | 如果两个角相等,则它们是对顶角 | |
| B. | 实数包括有理数、无理数 | |
| C. | 两直线被第三直线所截,内错角相等 | |
| D. | 若a2=b2,则a=b |
7. 如图.已知AB∥EF,∠BAE的平分线交EF于点C,∠E=64°,则∠ACE的度数为( )
如图.已知AB∥EF,∠BAE的平分线交EF于点C,∠E=64°,则∠ACE的度数为( )
 如图.已知AB∥EF,∠BAE的平分线交EF于点C,∠E=64°,则∠ACE的度数为( )
如图.已知AB∥EF,∠BAE的平分线交EF于点C,∠E=64°,则∠ACE的度数为( )| A. | 54° | B. | 58° | C. | 60° | D. | 64° |
8.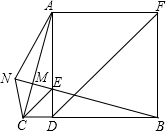 如图,已知正方形ADBF,点E在AD上,且∠AEB=105°,EC∥DF交BD的延长线于C,N为BE延长线上一点,BN交AC于M,且CE=2MN,连结AN、CN,下列结论:
如图,已知正方形ADBF,点E在AD上,且∠AEB=105°,EC∥DF交BD的延长线于C,N为BE延长线上一点,BN交AC于M,且CE=2MN,连结AN、CN,下列结论:
①AC⊥BN;②△NCE为等边三角形;③BF=2AM;④BE+$\sqrt{2}$DE=DF,
其中正确的有( )
 如图,已知正方形ADBF,点E在AD上,且∠AEB=105°,EC∥DF交BD的延长线于C,N为BE延长线上一点,BN交AC于M,且CE=2MN,连结AN、CN,下列结论:
如图,已知正方形ADBF,点E在AD上,且∠AEB=105°,EC∥DF交BD的延长线于C,N为BE延长线上一点,BN交AC于M,且CE=2MN,连结AN、CN,下列结论:①AC⊥BN;②△NCE为等边三角形;③BF=2AM;④BE+$\sqrt{2}$DE=DF,
其中正确的有( )
| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ②③④ |
9.若过点P和点A(3,2)的直线平行于x轴,过点P和B(-1,-2)的直线平行于y轴,则点P的坐标为( )
| A. | (-1,2 ) | B. | (-2,2) | C. | (3,-1) | D. | (3,-2) |

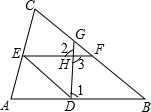 完成下面的证明过程
完成下面的证明过程 如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=8cm,AD=24cm,BC=26cm,点P从点A出发,以1cm/s的速度向点D运动;点Q从点C同时出发,以3cm/s的速度向点B运动.规定其中一个动点到达端点时,另一个动点也随之停止运动,设运动时间为t(s).
如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=8cm,AD=24cm,BC=26cm,点P从点A出发,以1cm/s的速度向点D运动;点Q从点C同时出发,以3cm/s的速度向点B运动.规定其中一个动点到达端点时,另一个动点也随之停止运动,设运动时间为t(s).