题目内容
9.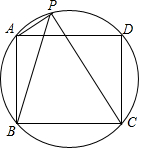 如图,已知P为正方形ABCD的外接圆的劣弧$\widehat{AD}$上任意一点,求证:$\frac{PA+PC}{PB}$为定值.
如图,已知P为正方形ABCD的外接圆的劣弧$\widehat{AD}$上任意一点,求证:$\frac{PA+PC}{PB}$为定值.
分析 首先根据题意画出图形,然后延长PA到E,使AE=PC,连接BE,易证得△ABE≌△CBP,继而可证得△BEP是等腰直角三角形,则可求得答案.
解答 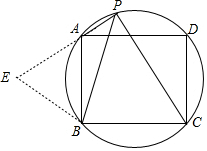 解:延长PA到E,使AE=PC,连接BE,
解:延长PA到E,使AE=PC,连接BE,
∵∠BAE+∠BAP=180°,∠BAP+∠PCB=180°,
∴∠BAE=∠PCB,
∵四边形ABCD是正方形,
∴AB=BC,∠ABC=90°,
在△ABE和△CBP中,
$\left\{\begin{array}{l}{AB=BC}\\{∠BAE=∠PCB}\\{AE=CP}\end{array}\right.$,
∴△ABE≌△CBP(SAS),
∴∠ABE=∠CBP,BE=BP,
∴∠ABE+∠ABP=∠ABP+∠CBP=90°,
∴△BEP是等腰直角三角形,
∴PA+PC=PE=$\sqrt{2}$PB.
即:$\frac{PA+PC}{PB}$=$\sqrt{2}$,
∴$\frac{PA+PC}{PB}$为定值.
点评 此题考查了圆的内接多边形的性质、正方形的性质、全等三角形的判定与性质以及等腰直角三角形性质.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
20.计算:$\frac{2x-6}{x-2}$÷$\frac{x-3}{{x}^{2}-4}$( )
| A. | 2x+4 | B. | 7 | C. | 5 | D. | 3 |
17.已知|a|=2,|b|=3,且|a+b|=|a|+|b|,则a+b的值为( )
| A. | 5 | B. | ±5 | C. | 1 | D. | ±1 |
14.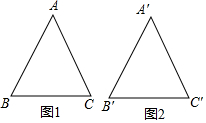 已知△ABC如图1所示,平平通过作图得到如图2所示的△A′B′C,其作图步骤为:
已知△ABC如图1所示,平平通过作图得到如图2所示的△A′B′C,其作图步骤为:
①画B′C′=BC;
②分别以点B′C′为圆心,线段AB,AC长为半径画弧,两弧交于点A′;
③连接A′B′,A′C′,则判断△ABC≌△A′B′C′的依据是( )
 已知△ABC如图1所示,平平通过作图得到如图2所示的△A′B′C,其作图步骤为:
已知△ABC如图1所示,平平通过作图得到如图2所示的△A′B′C,其作图步骤为:①画B′C′=BC;
②分别以点B′C′为圆心,线段AB,AC长为半径画弧,两弧交于点A′;
③连接A′B′,A′C′,则判断△ABC≌△A′B′C′的依据是( )
| A. | SSS | B. | SAS | C. | ASA | D. | AAS |
19.当x=1时,ax3-2bx+3=6,则当x=-1时,这个代数式的值是( )
| A. | 6 | B. | 0 | C. | -6 | D. | -3 |
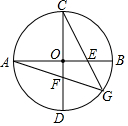 如图,已知圆O的直径AB与CD互相垂直,E为OB中点,CE的延长线交圆O于G,AG交CD于F,求$\frac{DF}{FC}$的值.
如图,已知圆O的直径AB与CD互相垂直,E为OB中点,CE的延长线交圆O于G,AG交CD于F,求$\frac{DF}{FC}$的值.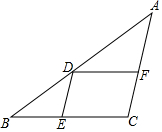 如图所示,在平行四边形DECF中,B是CE延长线上一点,BD的延长线交CF的延长线于点A.
如图所示,在平行四边形DECF中,B是CE延长线上一点,BD的延长线交CF的延长线于点A.