题目内容
1.填空:(1)直线y=4x-3经过点($\frac{3}{4}$,0)、(0,-3);
(2)直线y=-$\frac{1}{3}$x+2经过点(6,0)、(0,2)
分析 (1)将y=0代入解析式即可求出x的值,将x=0代入解析式即可求出y的值.
(2)将y=0代入解析式即可求出x的值,将x=0代入解析式即可求出y的值.
解答 解:(1)将y=0代入解析式得:4x-3=0,
解得x=$\frac{3}{4}$.
将x=0代入解析式得:y=-3,
故答案为$\frac{3}{4}$,-3;
(2)将y=0代入解析式得:-$\frac{1}{3}$x+2=0,
解得x=6.
将x=0代入解析式得:y=2,
故答案6,2.
点评 本题考查了一次函数图象上点的坐标特征,在这条直线上的各点的坐标一定适合这条直线的解析式.函数与y轴的交点的横坐标为0.函数与x轴的交点的纵坐标为0.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.n边形的对角线的总条数为m,则m=$\frac{n(n-3)}{2}$,其中自变量n的取值范围是( )
| A. | 全体实数 | B. | 全体整数 | ||
| C. | n≥3 | D. | 大于或等于3的整数 |
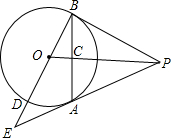 如图,PA为⊙O的切线,A为切点,过A作OP的垂线AB,垂足为点C,交⊙O于点B.延长BO与⊙O交于点B,延长BO与⊙O交于点D,与PA的延长线交于点E,
如图,PA为⊙O的切线,A为切点,过A作OP的垂线AB,垂足为点C,交⊙O于点B.延长BO与⊙O交于点B,延长BO与⊙O交于点D,与PA的延长线交于点E, 如图,梯形的上底长为3x,下底长为5x-y,高为3x+2y,求这个梯形的面积.
如图,梯形的上底长为3x,下底长为5x-y,高为3x+2y,求这个梯形的面积. 如图:△ABC中,AB=8,AC=6,BC=10,把△ABC沿DE对折,使得B,C重合,求AD的长.
如图:△ABC中,AB=8,AC=6,BC=10,把△ABC沿DE对折,使得B,C重合,求AD的长.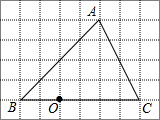 如图,在6×8的网格中,每个小正方形的边长均为1,点O和△ABC的顶点均为小正方形的顶点.
如图,在6×8的网格中,每个小正方形的边长均为1,点O和△ABC的顶点均为小正方形的顶点.